% A
% A
z F T 5 z " "
M 1 <
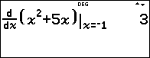
The TI-30X Pro MathPrint™ calculates the (approximate) numerical derivative of an expression at a point given a tolerance for the numerical method. (See the About the Numerical Derivative at a Point section for more information.)
% A pastes the numerical derivative template from the keypad to calculate the numerical derivative with the default tolerance H is 1EM5.
|
% A |
% A z F T 5 z " " M 1 < |
|
To change the default tolerance, H, and observe how the tolerance plays a role in the numerical solution, paste the numerical derivative from the menu location, d MATH 7:nDeriv(, where the numerical derivative template will paste with the option to modify the tolerance as needed for an investigation of the numerical derivative result.
|
d MATH 7:nDeriv( with optional tolerance |
d 7 z F T 5 z " " M 1 " 1 E M 5 < |
|
In Classic mode or in classic edit lines, the nDeriv( command will paste from the keypad or MATH menu.
Syntax: nDeriv(expression,variable,point[,tolerance]) where tolerance is optional and the default H is 1EM5.
|
% A or d MATH 7:nDeriv( |
% A z F T 5 z % ` z % ` M 1 ) < |
|
The numerical derivative at a point command, nDeriv( or d/dx, uses the symmetric difference quotient method. This method approximates the numerical derivative at a given point as the slope of the secant line about the point.
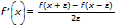
As H becomes smaller, the approximation usually becomes more accurate to approximate the slope of the tangent line at the given point x.
| • | Because of the method used to calculate the numerical derivative at a point, the calculator can return a false derivative value at a non-differentiable point. |
| • | Always have some knowledge of the function behaviour near the point by using a table of values near the point (or a graph of the function). |
Find the slope of the tangent line to the function f(x) = x2 - 4x at x = 2. What do you notice?
|
% A z F U 4 z " " 2 < |
|