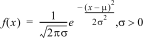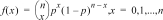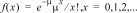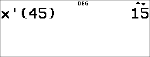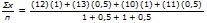Statistik, regressioner og fordelinger
v % u
Med v kan du indtaste og redigere datalisterne. (Se afsnittet Dataeditor).
% u viser -menuen, som indeholder følgende valg:
Noter:
|
•
|
Regressioner gemmer regressionsoplysningerne, sammen med 2-Var-statistikken for dataene, i StatVars (menupunkt 1). |
|
•
|
En regression kan gemmes i enten f(x) eller g(x). Regressionskoefficienterne vises med komplet nøjagtighed. |
Vigtig note om resultater: Mange af regressionsligningerne deler samme variabler , , og . Hvis du udfører en regressionsberegning, gemmes regressionsberegningen og 2-Var-statistikken for de pågældende data i -menuen, indtil den næste statistik- eller regressionsberegning. Resultaterne skal fortolkes baseret på, hvilken type statistik- eller regressionsberegning der er udført senest. For at gøre det nemmere at fortolke korrekt minder titellinjen om, hvilken beregning der er udført senest.
|
1:StatVars
|
Viser en sekundær menu med de senest beregnede statistiske resultatvariabler. Brug $ og # til at finde den ønskede variabel, og tryk på < for at markere den. Hvis du markerer dette valg, før du har beregnet 1-Var-statistik, 2-Var-statistik eller nogen af regressionerne, vises en påmindelse.
|
|
2:1-VAR STATS
|
Analyserer data fra 1 datasæt med 1 målt variabel, x. Der kan være medtaget frekvensdata.
|
|
3:2-VAR STATS
|
Analyserer parrede data fra 2 datasæt med 2 målte variabler – x, den uafhængige variabel, og y, den afhængige variabel. Der kan være medtaget hyppighedsdata.
Bemærk: 2-Var Stats beregner også en lineær regression og udfylder de lineære regressionsresultater. Den viser værdier for (hældning) og (y-skæring). Den viser også værdier for 2 og .
|
|
4:LinReg ax+b
|
Tilpasser ligningsmodellen y=ax+b til dataene med mindste kvadraters metode for mindst to datapunkter. Den viser værdier for (hældning) og (y-skæring). Den viser også værdier for 2 og .
|
|
5:PropReg ax
|
Tilpasser ligningsmodellen y=ax til dataene med mindste kvadraters metode for mindst et punkt. Den viser værdien for . Understøtter data, der danner en lodret linje med undtagelse af alle 0-data.
|
|
6:RecipReg a/x+b
|
Tilpasser ligningsmodellen y=a/x+b til dataene med mindste kvadraters metode på lineariserede data for mindst to datapunkter. Den viser værdier for og . Den viser også værdier for 2 og .
|
|
7:QuadraticReg
|
Tilpasser andengradspolynomiet y=ax2+bx+c til dataene. Den viser værdier for , og . Den viser også en værdi for 2. For tre datapunkter er ligningen en polynomietilpasning. For fire eller flere er den en polynomieregression. Mindst tre datapunkter er påkrævet.
|
|
8:CubicReg
|
Tilpasser tredjegradspolynomiet y=ax3+bx2+cx+d til dataene. Den viser værdier for , , , and . Den viser også en værdi for 2. For fire punkter er ligningen en polynomietilpasning. For fem eller flere er den en polynomieregression. Mindst fire punkter er påkrævet.
|
|
9:LnReg a+blnx
|
Tilpasser ligningsmodellen y=a+bln(x) til data med mindste kvadraters metode og transformerede værdier ln(x) og y Den viser værdier for og . Den viser også værdier for 2 og .
|
|
:PwrReg ax^b
|
Tilpasser ligningsmodellen y=axb til data med mindste kvadraters metode og transformerede værdier ln(x) og ln(y) Den viser værdier for og . Den viser også værdier for 2 og .
|
|
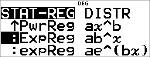
:ExpReg ab^x
|
Tilpasser ligningsmodellen y=abx til data med mindste kvadraters metode og transformerede værdier x og In(y). Den viser værdier for og . Den viser også værdier for 2 og .
|
|
:expReg ae^(bx)
|
Tilpasser ligningsmodellen y=a e^(bx) til dataene med mindste kvadraters metode på lineariserede data for mindst to datapunkter. Den viser værdier for og . Den viser også værdier for 2 og .
|
% u " viser -menuen, som indeholder følgende valg:
|
1:Normalpdf
|
Beregner sandsynlighedstæthedsfunktionen (pdf) for normalfordelingen ved en bestemt x-værdi. Standardindstillingerne er middelværdien mu=0 og standardafvigelsen sigma=1. Sandsynlighedstæthedsfunktionen (pdf) er:
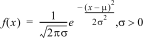
|
|
2:Normalcdf
|
Beregner den normale sandsynlighedsfordeling mellem LOWERbnd og UPPERbnd for den angivne middelværdi mu og standardafvigelsen sigma. Standarderne er mu=0, sigma=1, hvor LOWERbnd = M1E99 og UPPERbnd = 1E99.
Bemærk: M1E99 til 1E99 repræsenterer Muendelig til uendelig.
|
|
3:invNormal
|
Beregner den inverse kumulative normalfordelingsfunktion for et givet område under normalfordelingskurven angivet ved middelværdien mu og standardafvigelsen sigma. Den beregner den x-værdi, der er knyttet til et område til venstre for x-værdien. 0 { areal { 1 skal være sandt. Standarderne er areal=1, mu=0 og sigma=1.
|
|
4:Binomialpdf
|
Beregner en sandsynlighed på x for den diskrete binomialfordeling med de angivne numtrials og sandsynligheden for succes (p) for hvert forsøg. x er et ikke-negativt heltal og kan indtastes med valgmulighederne SINGLE (Enkelt indtastning), LIST (Liste over indtastninger) eller ALL (Alle) (liste over sandsynligheder fra 0 til numtrials returneres). 0 { p { 1 skal være sandt. Sandsynlighedstæthedsfunktionen () er:
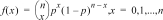
|
|
5:Binomialcdf
|
Beregner den kumulerede sandsynlighed på x for den diskrete binomialfordeling med de angivne numtrials og sandsynlighed for succes (p) for hvert forsøg. x kan være et ikke-negativt heltal og kan indtastes med valgmulighederne SINGLE (Enkelt indtastning), LIST (Liste) eller ALL (Alle) (en liste over kumulerede sandsynligheder returneres). 0 { p { 1 skal være sandt.
|
|
6:Poissonpdf
|
Beregner en sandsynlighed på x for den diskrete Poissonfordeling med den angivne middelværdi mu (m), som skal være et reelt tal > 0. x kan være et ikke-negativt heltal (SINGLE – Enkelt) eller en liste med heltal (LIST – Liste). Standardindstillingen er mu=1. Sandsynlighedstæthedsfunktionen () er:
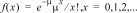
|
|
7:Poissoncdf
|
Beregner en kumuleret sandsynlighed på x for den diskrete Poissonfordeling med den angivne middelværdi mu, som skal være et reelt tal > 0. x kan være et ikke-negativt heltal (SINGLE – Enkelt) eller en liste med heltal (LIST – Liste). Standardindstillingen er mu=1.
|
Stats-resultater
|
|
1-Var
|
Antal x- eller (x,y)-datapunkter.
|
|
v
|
Begge
|
Gennemsnit af alle x-værdier.
|
|
w
|
2-Var
|
Gennemsnit af alle y-værdier.
|
|
|
Begge
|
Stikprøvestandardafvigelse for x.
|
|
|
2-Var
|
Stikprøvestandardafvigelse for y.
|
|
s
|
Begge
|
Populations standardafvigelse for x.
|
|
s
|
2-Var
|
Populations standardafvigelse for y.
|
|
G eller G2
|
Begge
|
Summen af alle x- eller x2-værdier.
|
|
G eller G2
|
2-Var
|
Summen af alle y- eller y2-værdier.
|
|
G
|
2-Var
|
Summen af (xQy) for alle xy-par.
|
|
|
2-Var
|
Lineær regression, hældning.
|
|
|
2-Var
|
Lineær regression, y-skæring.
|
|
2 eller
|
2-Var
|
Korrelationskoefficient.
|
|
¢
|
2-Var
|
Bruger a og b til at beregne den forventede x-værdi, når du angiver en y-værdi.
|
|
¢
|
2-Var
|
Bruger a og b til at beregne den forventede y-værdi, når du angiver en x-værdi.
|
|
eller
|
Begge
|
Minimum eller maksimum af x-værdier.
|
|
|
1-Var
|
Medianen for elementerne mellem minX og Med (1. kvartil).
|
|
|
1-Var
|
Median for alle datapunkter.
|
|
|
1-Var
|
Median for elementerne mellem Med og maxX (3. kvartil).
|
|
eller
|
2-Var
|
Minimum eller maksimum af y-værdier.
|
Sådan defineres statistiske datapunkter:
|
1.
|
Indtast data i L1, L2 eller L3. (Se afsnittet Dataeditor). |
Bemærk: ikke-heltalsfrekvenselementer er gyldige. Dette er praktisk ved indtastning af frekvenser udtrykt som procenttal eller dele, der til sammen giver 1. Stikprøvestandardafvigelsen, Sx, er dog udefineret for ikke-heltalsfrekvenser, og Sx=Error (Sx=Fejl) vises for den pågældende værdi. Alle andre statistikker vises.
|
2.
|
Tryk på % u. Marker eller , og tryk på <. |
|
3.
|
Marker L1, L2 eller L3 samt frekvensen. |
|
4.
|
Tryk på < for at få vist menuen med variablerne. |
|
5.
|
Du kan slette data ved at trykke på v v, markere en liste, der skal slettes, og trykke på <. |
1-Var-eksempel
Find gennemsnittet af {45,55,55,55}
|
Slet alle data
|
v v $ $ $
|
|
|
Data
|
<
$ $ $
<
|

|
|
Statistik
|
% s
% u
|

|
|
|
(markerer )
$ $
|
|
|
|
<
|

|
|
Stat Var
|
<
|

|
|
|
V <
|

|
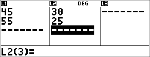
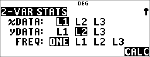
2-Var-eksempel
Data: (45,30); (55,25). Find: x¢(45).
|
Slet alle data
|
v v $ $ $
|

|
|
Data
|
< $ $ " $ $
|
|
|
Statistik
|
% u
|

|
|
|
(markerer )
$ $ $
|
|
|
StatVars
|
< % s
% u
# # # # # #
|
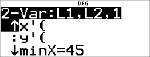
|
|
|
< ) <
|
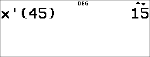
|
³ Opgave
I sine sidste fire tests opnåede Anton følgende point: Test nr. 2 og 4 blev tildelt vægten 0,5, og test 1 og 3 blev tildelt vægten 1.
|
Test nr.
|
1
|
2
|
3
|
4
|
|
Point
|
12
|
13
|
10
|
11
|
|
Vægt
|
1
|
0,5
|
1
|
0,5
|
|
1.
|
Find Antons pointgennemsnit (vægtede gennemsnit). |
|
2.
|
Hvad angiver værdien af n på lommeregneren? Hvad angiver værdien af Gx på lommeregneren? |
Husk: Det vægtede gennemsnit er
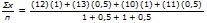
|
3.
|
Læreren gav Anton 4 point mere i test nr. 4 på grund af en vægtningsfejl. Find Antons nye pointgennemsnit. |
|
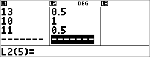
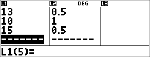
v v $ $ $
|

|
|
<
v " $ $ $ $
|
|
|
<
$ $ $ $
" $ $ $
<
|
|
|
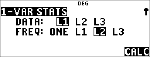
% u
|

|
|
$ " " <
|
|
|
<
|
|
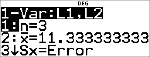
Anton har et gennemsnit (v) på 11,33 (tilnærmet til nærmeste hundrededel).
På lommeregneren repræsenterer n den samlede sum af vægtene.
n = 1 + 0.5 + 1 + 0.5.
Gx repræsenterer den vægtede sum af hans point.
(12)(1) + (13)(0.5) + (10)(1) + (11)(0.5) = 34.
Forhøj Antons sidste point fra 11 til 15.
|
v $ $ $ <
|
|
|
% u
$ " " < <
|

|
Hvis læreren tilføjer 4 point til Test nr. 4, er Antons gennemsnit 12.
³ Opgave
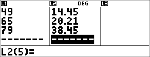
Nedenstående tabel gengiver resultaterne af en bremsetest.
|
Test nr.
|
1
|
2
|
3
|
4
|
|
Hastighed (km/t)
|
33
|
49
|
65
|
79
|
|
Bremselængde (m)
|
5,30
|
14,45
|
20,21
|
38,45
|
Brug sammenhængen mellem hastighed og bremselængde til at vurdere bremselængden for en bil, der kører 55 km/t.
Et håndtegnet punktdiagram med disse datapunkter antyder en lineær sammenhæng. Lommeregneren benytter mindste kvadraters metode til at finde den bedste rette linje, y'=ax'+b, for data, der indtastes på lister.
|
v v $ $ $
|

|
|
<
$ $ $ $ " $ $ $ <
|
|
|
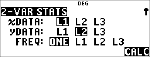
% s
% u
|

|
|
(markerer )
$ $ $
|
|
|
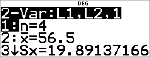
<
|
|
|
Tryk på $ efter behov for at få vist a og b.
|
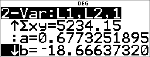
|
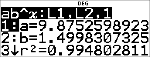
Denne bedste rette linje, y'=0.67732519x'N18.66637321 modellerer den lineære tendens i dataene.
|
Tryk på $, indtil y' er fremhævet.
|

|
|
< ) <
|

|
Den lineære model giver en vurderet bremselængde på 18,59 meter for en bil, der kører 55 km/t.
Regressionseksempel 1
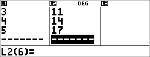
Beregn en ax+b lineær regression for følgende data: {1,2,3,4,5}; {5,8,11,14,17}.
|
Slet alle data
|
v v $ $ $
|

|
|
Data
|
<
$ $ $ $
$ "
$ $ $ $
<
|
|
|
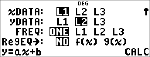
Regression
|
% s
% u
$ $ $
|

|
|
|
<
|
|
|
|
$ $ $ $
<
Tryk på $ for at undersøge alle resultatvariabler.
|

|
Regressionseksempel 2
Beregn den eksponentielle regression for følgende data:
|
•
|
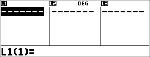
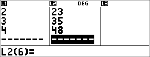
L1 = {0,1,2,3,4}; L2 = {10,14,23,35,48} |
|
•
|
Find gennemsnitsværdien for dataene i L2. |
|
•
|
Sammenlign de eksponentielle regressionsværdier med L2. |
|
Slet alle data
|
v v
|
|
|
Data
|
$ $ $ $
$ " $ $ $ $ <
|
|
|
Regression
|
% u
# #
|
|
|
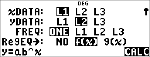
Gem regressionsligningen
i f(x) i I-menuen.
|
< $ $ $ "
<
|
|
|
Regressionsligning
|
<
|
|
|
Find gennemsnitsværdien (y) for dataene i L2 ved hjælp af StatVars.
|
% u
(Vælger )
$ $ $
$ $ $
$ $
|
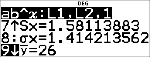
Bemærk, at titellinjen minder dig om din seneste statistik- eller regressionsberegning.
|
|
Undersøg tabellen over værdier for regressionsligningen.
|
I
|

|
|
|
< $
<
<
|

|
|
|
< <
|
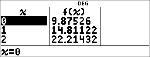
|
Advarsel: Hvis du nu beregner 2-Var Stats på dine data, beregnes variablerne og (sammen med og 2) som en lineær regression. Hvis du vil bevare dine regressionskoefficienter (a, b, c, d) og r-værdier for den specifikke opgave i -menuen, skal du ikke genberegne 2-Var Stats efter en anden regressionsberegning.
Fordelingseksempel
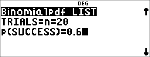
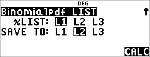
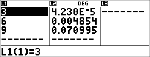
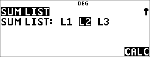
Beregn binomial-pdf-fordeling ved x-værdier {3,6,9} med 20 prøver og en successandsynlighed på 0,6. Indtast x-værdierne på liste L1, gem resultaterne i L2, find derefter summen af sandsynlighederne, og gem dem i variablen t.
|
Slet alle data
|
v v $ $ $
|

|
|
Data
|
<
$ $
<
|
|
|
DISTR
|
% u "
$ $ $
|

|
|
|
< "
|
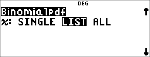
|
|
|
<
$
|
|
|
|
< $ $
|
|
|
|
<
|
|
|
|
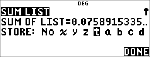
v ! "
<
|
|
|
|
<
" " " "
< <
|
|