% Q
q " <
% Q
0 " g " "
z X z ) "
<
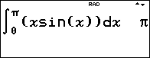
% Q indsætter skabelonen for det numeriske integral fra tastaturet for at beregne det numeriske integral med standardtolerancen H er 1EM5.
|
% Q |
q " < % Q 0 " g " " z X z ) " < |
|
Hvis du vil ændre standardtolerancen, H, og observere, hvilken rolle tolerance spiller i den numeriske løsning, skal du indsætte det numeriske integral fra menuplaceringen, d MATH 8:fnInt(, hvor skabelonen for det numeriske integral indsættes med mulighed for at ændre tolerancen efter behov, så resultatet af det numeriske integral kan undersøges.
|
d MATH 8:fnInt( med valgfri tolerance |
q < d 8 0 " 3 " z G 5 < |
|
I Classic-tilstand eller på classic-redigeringslinjer indsættes kommandoen fnInt( fra tastaturet eller menuen MATH (Matematik).
Syntaks: fnInt(udtryk,variabel,øvre,nedre[,tolerance]), hvor tolerance er valgfri, og standarden H er 1EM5.
|
% Q eller d MATH 8:fnInt( |
% Q z G 5 % . z % .0 % .3 ) < |
|
Find området under kurven f(x) = Mx2+4 på x-intervallerne fra M2 til 0 og derefter fra 0 til 2. Hvad lægger du mærke til ved resultaterne? Hvad kan du sige om denne funktions graf?
|
% Q M 2 " 0 " M z F T 4 " r |
|
|
< |
|
|
# # < % ! " 0 J " 2 |
|
|
< |
|
Bemærk, at de to områder er ens. Fordi dette er en parabel med toppunktet ved (0,4) og nuller ved (M2,0) og (2,0), kan du se, at de symmetriske områder er ens.