% A
% A
z F T 5 z " "
M 1 <
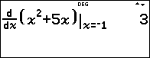
TI-30X Pro MathPrint™ beregner den (omtrentlige) numeriske differentialkvotient af et udtryk i et punkt med en given tolerance for den numeriske metode. (Se afsnittet Om den numeriske differentialkvotient i et punkt for at få flere oplysninger).
% A indsætter skabelonen for den numeriske differentialkvotient fra tastaturet for at beregne den numeriske differentialkvotient med standardtolerancen H er 1EM5.
|
% A |
% A z F T 5 z " " M 1 < |
|
Hvis du vil ændre standardtolerancen, H, og observere, hvilken rolle tolerancen spiller i den numeriske løsning, skal du indsætte den numeriske differentialkvotient fra menuplaceringen, d MATH 7:nDeriv(, hvor skabelonen for den numeriske differentialkvotient indsættes med mulighed for at ændre tolerancen efter behov, så resultatet af den numeriske differentialkvotient kan undersøges.
|
d MATH 7:nDeriv( med valgfri tolerance |
d 7 z F T 5 z " " M 1 " 1 E M 5 < |
|
I Classic-tilstand eller på classic-redigeringslinjer indsættes kommandoen nDeriv( fra tastaturet eller menuen MATH (Matematik).
Syntaks: nDeriv(udtryk,variabel,punkt[,tolerance]), hvor tolerance er valgfri, og standarden H er 1EM5.
|
% A eller d MATH 7:nDeriv( |
% A z F T 5 z % ` z % ` M 1 ) < |
|
Kommandoen for den numeriske differentialkvotient i et punkt, nDeriv( eller d/dx, benytter den symmetriske differenskvotientmetode. Denne metode tilnærmer sig den numeriske differentialkvotient i et bestemt punkt som hældningen på sekanten omkring punktet.
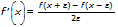
Når H bliver mindre, bliver tilnærmelsen normalt mere nøjagtig i forhold til hældningen på tangentlinjen i det pågældende punkt x.
| • | På grund af den metode, der benyttes til at beregne numeriske differentialkvotient, kan lommeregneren fejlagtigt give en differentialkvotient i et punkt, hvor funktionen ikke er differentiabel. |
| • | Sørg for altid at vide noget om funktionens adfærd nær punktet ved at bruge en tabel over værdier nær punktet (eller en graf for funktionen). |
Find hældningen på tangentlinjen for funktionen f(x) = x2 - 4x ved x = 2. Hvad lægger du mærke til?
|
% A z F U 4 z " " 2 < |
|