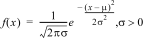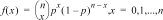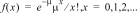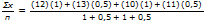Statistiques, régressions et distributions
v % u
v vous permet de saisir et de modifier les listes de données. (Voir la section relative à l'éditeur de données.)
% u affiche le menu , qui comporte les options suivantes.
Remarques :
|
•
|
Les régressions conservent les informations de régression, ainsi que les statistiques 2-Var des données, dans StatVars (1er élément de menu). |
|
•
|
Une régression peut être affectée à f(x) ou g(x). Les coefficients de régression s'affichent selon la précision maximale. |
Remarque importante concernant les résultats : De nombreuses équations de régression ont en commun les mêmes variables , , et . Si vous calculez une régression, le calcul et les variables statistiques 2-Var des données correspondantes figurent dans le menu jusqu'au prochain calcul statistique ou de régression. Il convient d'interpréter les résultats en fonction du dernier type de calcul statistique ou du dernier calcul de régression effectué. Pour faciliter l'interprétation, la barre de titre vous rappelle le dernier calcul effectué.
|
1 : StatVars
|
Affiche un menu secondaire des dernières variables de résultats statistiques calculées. Utilisez $ et # pour repérer la variable désirée, puis appuyez sur < pour la sélectionner. Si vous sélectionnez cette option avant de calculer les variables de statistiques 1-Var stats, 2-Var stats, ou l'une des régressions, un rappel s'affiche à l'écran.
|
|
2 : 1-VAR STATS
|
Analyse les données statistiques à partir d'un ensemble de données avec une variable mesurée, x. Il est possible d'y inclure les données de fréquence.
|
|
3 : 2-VAR STATS
|
Analyse les données par paires de deux ensembles de données avec deux variables mesurées, x, la variable indépendante, et y, la variable dépendante. Il est possible d'y inclure les données de fréquence.
Remarque : 2-Var Stats permet par ailleurs de calculer une régression linéaire et remplit les résultats correspondants. Elle affiche les valeurs pour (la pente) et (ordonnée à l'origine), de même que les valeurs pour 2 et .
|
|
4 : LinReg ax+b
|
Ajuste l'équation modèle y=ax+b aux données en utilisant la méthode des moindres carrés pour au moins deux points de données. Elle affiche les valeurs pour (la pente) et (ordonnée à l'origine), de même que les valeurs pour 2 et .
|
|
5 : PropReg ax
|
Ajuste l'équation modèle y=ax aux données en utilisant la méthode des moindres carrés pour au moins un point de données. Elle affiche la valeur pour . Prend en charge les données formant une droite verticale, à l'exception de toutes les données égales à 0.
|
|
6 : RecipReg a/x+b
|
Ajuste l'équation modèle y=a/x+b aux données en appliquant la méthode des moindres carrés aux données linéarisées pour au moins deux points de données. Elle affiche les valeurs pour et , de même que les valeurs pour 2 et .
|
|
7 : QuadraticReg
|
Ajuste le polynôme du second degré y=ax2+bx+c aux données. Elle affiche les valeurs pour , et , de même qu'une valeur pour 2. Pour trois points de données, l'équation correspond à un ajustement polynomial ; pour quatre points ou plus, il s'agit d'une régression polynomiale. Trois points de données au minimum sont nécessaires.
|
|
8 : CubicReg
|
Ajuste le polynôme du troisième degré y=ax3+bx2+cx+d aux données. Elle affiche les valeurs pour , , et , de même qu'une valeur pour 2. Pour quatre points de données, l'équation correspond à un ajustement polynomial ; pour cinq points ou plus, il s'agit d'une régression polynomiale. Quatre points au minimum sont nécessaires.
|
|
9 : LnReg a+blnx
|
Ajuste l'équation modèle y=a+b ln(x) aux données en appliquant la méthode des moindres carrés et les valeurs transformées ln(x) et y. Elle affiche les valeurs pour et , de même que les valeurs pour 2 et .
|
|
: PwrReg ax^b
|
Ajuste l'équation modèle y=axb aux données en appliquant la méthode des moindres carrés et les valeurs transformées ln(x) et ln(y). Elle affiche les valeurs pour et , de même que les valeurs pour 2 et .
|
|
: ExpReg ab^x
|
Ajuste l'équation modèle y=abx aux données en appliquant la méthode des moindres carrés et les valeurs transformées x et ln (y). Elle affiche les valeurs pour et , de même que les valeurs pour 2 et .
|
|
: expReg ae^(bx)
|
Ajuste l'équation modèle y=a e^(bx) aux données en appliquant la méthode des moindres carrés aux données linéarisées pour au moins deux points de données. Elle affiche les valeurs pour et , de même que les valeurs pour 2 et .
|
% u " affiche le menu , qui comporte les fonctions de distribution suivantes :
|
1 : Normalpdf
|
Calcule la fonction de densité de probabilité (pdf) de la loi normale à la valeur x spécifiée. Par défaut, la moyenne mu=0 et l'écart type sigma=1. La fonction de densité de probabilité (pdf) est la suivante :
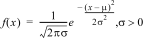
|
|
2 : Normalcdf
|
Calcule la probabilité pour la loi normale définie par les limites LOWERbnd et UPPERbnd pour la moyenne mu et l'écart type sigma indiqués. Les valeurs par défaut sont mu=0 ; sigma=1 ; avec les paramètres LOWERbnd = M1E99 et UPPERbnd = 1E99.
Remarque : M1E99 à 1E99 représente l'infini négatif M à l'infini positif.
|
|
3 : invNormal
|
Calcule la réciproque de la fonction de répartition pour une aire donnée avec la courbe de répartition normale spécifiée par la moyenne mu et l'écart type sigma. Elle calcule la valeur x associée à une aire située à gauche de la valeur x. 0 { aire { 1 doit être vrai. Les valeurs par défaut sont aire=1, mu=0 et sigma=1.
|
|
4 : Binomialpdf
|
Calcule la probabilité de x pour la loi binomiale discrète avec le nombre d'essais numtrials et la probabilité de réussite (p) pour chaque essai indiqués. x est un entier non négatif qui peut être spécifié avec les options d'entrée suivantes : SINGLE, LIST ou ALL (renvoi de la liste de probabilités de 0 au nombre d'essais numtrials). 0 { p { 1 doit être vrai. La fonction de densité de probabilité () est la suivante :
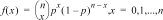
|
|
5 : Binomialcdf
|
Calcule la probabilité cumulée de x pour la loi binomiale discrète avec le nombre d'essais numtrials et la probabilité de réussite (p) pour chaque essai indiqués. x peut être un entier non négatif et spécifié avec les options d'entrée suivantes : SINGLE, LIST ou ALL (renvoi d'une liste de probabilités cumulées). 0 { p { 1 doit être vrai.
|
|
6 : Poissonpdf
|
Calcule la probabilité de x pour la loi de Poisson discrète avec la moyenne mu spécifiée (m), qui doit être un nombre réel > 0. x peut être un entier non négatif (SINGLE) ou une liste d'entiers (LIST). Le paramètre par défaut est mu=1. La fonction de densité de probabilité () est la suivante :
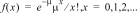
|
|
7 : Poissoncdf
|
Calcule la probabilité cumulée de x pour la loi de Poisson discrète avec la moyenne mu spécifiée, qui doit être un nombre réel > 0. x peut être un entier non négatif (SINGLE) ou une liste d'entiers (LIST). Le paramètre par défaut est mu=1.
|
Résultats statistiques
|
|
1-Var
|
Nombre de points de données x ou (x,y).
|
|
v
|
Les deux
|
Moyenne de toutes les valeurs x.
|
|
w
|
2-Var
|
Moyenne de toutes les valeurs y.
|
|
|
Les deux
|
Écart-type d'échantillon de x.
|
|
|
2-Var
|
Écart-type d'échantillon de y.
|
|
s
|
Les deux
|
Écart-type de population de x.
|
|
s
|
2-Var
|
Écart-type de population de y.
|
|
G ou G2
|
Les deux
|
Somme de toutes les valeurs x ou x2.
|
|
G ou G2
|
2-Var
|
Somme de toutes les valeurs y ou y2.
|
|
G
|
2-Var
|
Somme de (xQy) pour toutes les paires xy.
|
|
|
2-Var
|
Pente de la droite de régression linéaire.
|
|
|
2-Var
|
Ordonnée à l'origine y de la régression linéaire.
|
|
2 ou
|
2-Var
|
Coefficient de corrélation.
|
|
¢
|
2-Var
|
Utilise a et b pour calculer la valeur x prévue lorsque vous entrez une valeur y.
|
|
¢
|
2-Var
|
Utilise a et b pour calculer la valeur y prévue lorsque vous entrez une valeur x.
|
|
ou
|
Les deux
|
Minimum ou maximum des valeurs x.
|
|
|
1-Var
|
Valeur médiane des éléments compris entre minX et Med (1er quartile).
|
|
|
1-Var
|
Valeur médiane de tous les points de données.
|
|
|
1-Var
|
Valeur médiane des éléments compris entre Med et maxX (3e quartile).
|
|
ou
|
2-Var
|
Minimum ou maximum des valeurs y.
|
Pour définir les points de données statistiques :
|
1.
|
Entrez les données dans L1, L2 ou L3. (Voir la section relative à l'éditeur de données.) |
Remarque : Les éléments de fréquence non entiers sont valables. Ceci est pratique pour la saisie de fréquences exprimées sous forme de pourcentages ou de valeurs qui, une fois additionnées, sont égales à 1. Cependant, l'écart type d'échantillon, Sx, n'est pas défini pour les fréquences non entières, et le message Sx=Error s'affiche en regard de cette valeur. Toutes les autres statistiques sont affichées.
|
2.
|
Appuyez sur % u. Sélectionnez ou , puis appuyez sur <. |
|
3.
|
Sélectionnez L1, L2 ou L3, puis la fréquence. |
|
4.
|
Appuyez sur < pour afficher le menu des variables. |
|
5.
|
Pour effacer des données, appuyez sur v v, sélectionnez la liste à effacer, puis appuyez sur <. |
Exemple avec 1-Var
Calculez la moyenne de {45,55,55,55}.
|
Effacer toutes les données
|
v v $ $ $
|
|
|
Données
|
<
$ $ $
<
|

|
|
Stat
|
% s
% u
|

|
|
|
(active )
$ $
|
|
|
|
<
|

|
|
Stat Var
|
<
|

|
|
|
V <
|

|
Exemple avec 2-Var
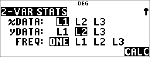
Données : (45,30); (55,25). Calculez : x¢(45).
|
Effacer toutes les données
|
v v $ $ $
|

|
|
Données
|
< $ $ " $ $
|
|
|
Stat
|
% u
|

|
|
|
(active )
$ $ $
|
|
|
StatVars
|
< % s
% u
# # # # # #
|
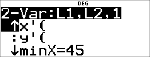
|
|
|
< ) <
|
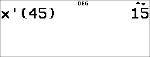
|
³ Activité
À ses quatre derniers contrôles, Anthony a obtenu les notes suivantes. Les contrôles 2 et 4 avaient un coefficient de 0,5, tandis que les contrôles 1 et 3 avaient un coefficient de 1.
|
N° du test
|
1
|
2
|
3
|
4
|
|
Note
|
12
|
13
|
10
|
11
|
|
Coef. de pondération
|
1
|
0,5
|
1
|
0,5
|
|
1.
|
Calculez la moyenne d'Anthony (moyenne pondérée). |
|
2.
|
Que représente la valeur n donnée par la calculatrice ? Que représente la valeur G donnée par la calculatrice ? |
Rappel : La moyenne pondérée est égale à
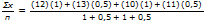
|
3.
|
Le professeur a donné à Anthony 4 points de plus au contrôle 4 suite à une erreur de notation. Calculez la nouvelle moyenne d'Anthony. |
|
v v $ $ $
|

|
|
<
v " $ $ $ $
|
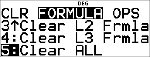
|
|
<
$ $ $ $
" $ $ $
<
|
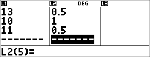
|
|
% u
|

|
|
$ " " <
|
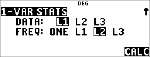
|
|
<
|
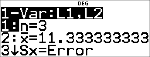
|
Anthony a une moyenne (v) de 11,33 (note arrondie au centième le plus proche).
Sur la calculatrice, n représente la somme totale des coefficients de pondération.
n = 1 + 0.5 + 1 + 0.5.
Gx représente la somme pondérée des notes de l'élève.
(12)(1) + (13)(0.5) + (10)(1) + (11)(0.5) = 34.
Modifiez la dernière note d'Anthony de 11 à 15.
|
v $ $ $ <
|
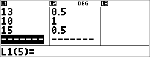
|
|
% u
$ " " < <
|

|
Si le professeur ajoute 4 points au 4e contrôle, la moyenne d'Anthony passe à 12.
³ Activité
Le tableau ci-dessous présente les résultats d'une série d'essais de freinage.
|
N° du test
|
1
|
2
|
3
|
4
|
|
Vitesse (km/h)
|
33
|
49
|
65
|
79
|
|
Distance de freinage (m)
|
5,30
|
14,45
|
20,21
|
38,45
|
En utilisant la relation entre la vitesse et la distance de freinage, calculez la distance de freinage nécessaire à un véhicule se déplaçant à 55 km/h.
Un nuage de points tracé à la main à partir de ces données suggère un relation linéaire. La calculatrice utilise la méthode des moindres carrés pour calculer la droite de régression, y'=ax'+b, à partir des données saisies dans les listes.
|
v v $ $ $
|

|
|
<
$ $ $ $ " $ $ $ <
|
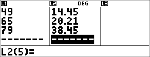
|
|
% s
% u
|

|
|
(active )
$ $ $
|
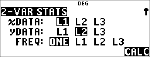
|
|
<
|
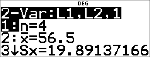
|
|
Appuyez au besoin sur $ pour afficher a et b.
|
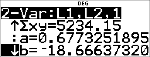
|
Cette droite de régression, y'=0.67732519x'N18.66637321 définit la forme de la tendance linéaire des données.
|
Appuyez sur $ jusqu'à ce que y' soit mis en surbrillance.
|

|
|
< ) <
|

|
Le modèle linéaire estime la distance de freinage à 18,59 mètres pour un véhicule se déplaçant à 55 km/h.
Exemple de régression 1
Calculez une régression linéaire ax+b pour les données suivantes : {1,2,3,4,5} ; {5,8,11,14,17}.
|
Effacer toutes les données
|
v v $ $ $
|

|
|
Données
|
<
$ $ $ $
$ "
$ $ $ $
<
|
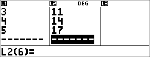
|
|
Régression
|
% s
% u
$ $ $
|

|
|
|
<
|
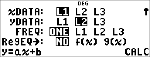
|
|
|
$ $ $ $
<
Appuyez sur $ pour examiner toutes les variables du résultat.
|

|
Exemple de régression 2
Calculez la régression exponentielle pour les données suivantes :
|
•
|
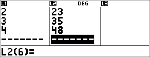
L1 = {0,1,2,3,4} ; L2 = {10,14,23,35,48} |
|
•
|
Calculez la valeur moyenne des données de L2. |
|
•
|
Comparez les valeurs de régression exponentielle pour L2. |
|
Effacer toutes les données
|
v v
|
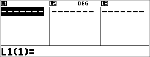
|
|
Données
|
$ $ $ $
$ " $ $ $ $ <
|
|
|
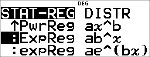
Régression
|
% u
# #
|
|
|
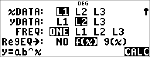
Enregistrez l'équation de régression
dans f(x) via le menu I.
|
< $ $ $ "
<
|
|
|
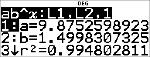
Équation de régression
|
<
|
|
|
Calculez la valeur moyenne (y) des données de L2 à l'aide de StatVars.
|
% u
(active )
$ $ $
$ $ $
$ $
|
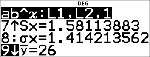
Notez que la barre de titre vous rappelle le dernier calcul de régression ou statistique effectué.
|
|
Examinez le tableau de valeurs de l'équation de régression.
|
I
|

|
|
|
< $
<
<
|

|
|
|
< <
|
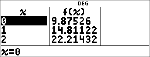
|
Attention: Si vous appliquez à présent 2-Var Stats à vos données, les variables et (de même que et 2) seront calculées sous forme de régression linéaire. N'appliquez plus 2-Var Stats après tout autre calcul de régression si vous souhaitez conserver vos coefficients de régression (a, b, c, d) et valeurs r pour un exercice précis dans le menu .
Exemple de distribution
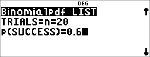
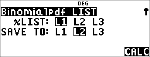
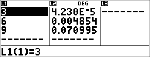
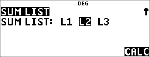
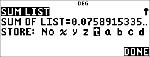
Calculez la distribution pdf binomiale des valeurs x {3,6,9} avec 20 essais et une probabilité de réussite de 0,6. Entrez les valeurs x dans la liste L1, stockez les résultats dans L2, puis calculez la somme des probabilités et enregistrez-la dans la variable t.
|
Effacer toutes les données
|
v v $ $ $
|

|
|
Données
|
<
$ $
<
|
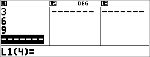
|
|
DISTR
|
% u "
$ $ $
|

|
|
|
< "
|
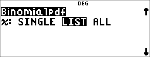
|
|
|
<
$
|
|
|
|
< $ $
|
|
|
|
<
|
|
|
|
v ! "
<
|
|
|
|
<
" " " "
< <
|
|