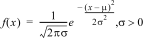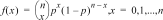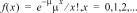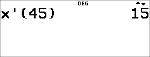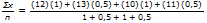Statistik, Regressionen und Verteilungen
v % u
v ermöglicht es Ihnen, Daten in Listen einzugeben und anschließend zu bearbeiten. (Siehe Abschnitt „Dateneditor“.)
% u öffnet das Menü mit den folgenden Optionen.
Hinweise:
|
•
|
Bei Regressionen werden die Regressionsdaten sowie die bivariaten Statistikangaben für die Daten in StatVars gespeichert (Menüeintrag 1). |
|
•
|
Eine Regression kann entweder in f(x) oder g(x) gespeichert werden. Die Regressionskoeffizienten werden mit maximaler Präzision angezeigt. |
Wichtiger Hinweis zu den Ergebnissen: Viele Regressionsgleichungen verwenden dieselben Variablen , , und . Nach einer Regressionsberechnung bleiben diese und die bivariaten Statistikangaben für die betreffenden Daten im Menü gespeichert, bis Sie die nächste Statistik- oder Regressionsberechnung durchführen. Bei der Interpretation der Ergebnisse muss daher berücksichtigt werden, welche Statistik- oder Regressionsberechnung zuletzt durchgeführt wurde. Als Hilfestellung wird dies in der Titelleiste angezeigt.
|
1:StatVars
|
Zeigt ein Untermenü mit den zuletzt berechneten statistischen Ergebnisvariablen an. Markieren Sie mit $ und # die gewünschte Variable und drücken Sie <, um sie auszuwählen. Wenn Sie diese Option wählen, bevor Sie die univariaten/bivariaten Statistikangaben oder eine Regression berechnet haben, wird ein entsprechender Hinweis gegeben.
|
|
2:1-VAR STATS
|
Analysiert statistische Daten aus einem einzigen Datensatz mit einer Messvariablen, x. Häufigkeitsdaten können ebenfalls enthalten sein.
|
|
3:2-VAR STATS
|
Analysiert Datenpaare aus zwei Datensätzen mit zwei Messvariablen: der unabhängigen Variablen x und der abhängigen Variablen y. Häufigkeitsdaten können ebenfalls enthalten sein.
Hinweis: Die Funktion „2-Var Stats“ berechnet außerdem die lineare Regression und gibt das Ergebnis in dem entsprechenden Feld an. Die Funktion zeigt Werte für (Steigung) und (y-Achsenabschnitt) an, außerdem Werte für 2 und .
|
|
4:LinReg ax+b
|
Passt die Modellgleichung y=ax+b nach der Methode der kleinsten Quadrate an die Daten an (bei mindestens zwei Datenpunkten). Die Funktion zeigt Werte für (Steigung) und (y-Achsenabschnitt) an, außerdem Werte für 2 und .
|
|
5:PropReg ax
|
Passt die Modellgleichung y=ax nach der Methode der kleinsten Quadrate an die Daten an (bei mindestens einem Datenpunkt). Die Funktion zeigt den Wert für an. Unterstützt Daten, die eine vertikale Gerade bilden, mit Ausnahme aller 0-Daten.
|
|
6:RecipReg a/x+b
|
Passt die Modellgleichung y=a/x+b nach der Methode der kleinsten Quadrate an die Daten an (bei linearisierten Daten bei mindestens zwei Datenpunkten). Die Funktion zeigt Werte für und an, außerdem Werte für 2 und .
|
|
7:QuadraticReg
|
Passt das Polynom zweiten Grades y=ax2+bx+c an die Daten an. Die Funktion zeigt Werte für , und an, außerdem einen Wert für 2. Bei drei Datenpunkten ist die Gleichung eine Polynom-Anpassung; bei vier oder mehr Datenpunkten wird eine Polynom-Regression verwendet. Es werden mindestens drei Datenpunkte benötigt.
|
|
8:CubicReg
|
Passt das Polynom dritten Grades y=ax3+bx2+cx+d an die Daten an. Die Funktion zeigt Werte für , , und an, außerdem einen Wert für 2. Bei vier Punkten ist die Gleichung eine Polynom-Anpassung; bei fünf oder mehr Punkten wird eine Polynom-Regression verwendet. Es werden mindestens vier Punkte benötigt.
|
|
9:LnReg a+blnx
|
Passt die Modellgleichung y=a+b ln(x) nach der Methode der kleinsten Quadrate und mit den umgewandelten Werten ln(x) und y an die Daten an. Die Funktion zeigt Werte für und an, außerdem Werte für 2 und .
|
|
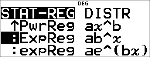
:PwrReg ax^b
|
Passt die Modellgleichung y=axb nach der Methode der kleinsten Quadrate und mit den umgewandelten Werten ln(x) und ln(y) an die Daten an. Die Funktion zeigt Werte für und an, außerdem Werte für 2 und .
|
|
:ExpReg ab^x
|
Passt die Modellgleichung y=abx nach der Methode der kleinsten Quadrate und mit den umgewandelten Werten x und ln(y) an die Daten an. Die Funktion zeigt Werte für und an, außerdem Werte für 2 und .
|
|
:expReg ae^(bx)
|
Passt die Modellgleichung y=a e^(bx) nach der Methode der kleinsten Quadrate an die Daten an (bei linearisierten Daten bei mindestens zwei Datenpunkten). Die Funktion zeigt Werte für und an, außerdem Werte für 2 und .
|
% u " öffnet das Menü mit den folgenden Funktionen für Verteilungen:
|
1:Normalpdf
|
Berechnet die Wahrscheinlichkeitsdichtefunktion (pdf) für die Normalverteilung für einen bestimmten x-Wert. Die Standardwerte sind Mittelwert mu=0 und Standardabweichung sigma=1. Die Wahrscheinlichkeitsdichtefunktion (pdf) lautet:
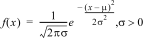
|
|
2:Normalcdf
|
Berechnet für eine normalverteilte Zufallsgröße die kumulierte Wahrscheinlichkeit für den Bereich zwischen einer anzugebenden Untergrenze (LOWERbnd) und einer Obergrenze (UPPERbnd) für den anzugebenden Mittelwert mu und die Standardabweichung sigma. Die Standardwerte sind: mu=0; sigma=1; LOWERbnd = M1E99; UPPERbnd = 1E99.
Hinweis: M1E99 bis 1E99 entspricht Munendlich bis unendlich.
|
|
3:invNormal
|
Berechnet die inverse kumulative Normalverteilungsfunktion für eine bestimmte Fläche unter der Normalverteilungskurve, die durch den Mittelwert mu und die Standardabweichung sigma festgelegt ist. Die Funktion berechnet den x-Wert, der zu einer Fläche gehört, die sich links vom x-Wert befindet. 0 { Fläche { 1 muss wahr sein. Die Standardwerte sind Fläche=1, mu=0 und sigma=1.
|
|
4:Binomialpdf
|
Berechnet die Wahrscheinlichkeit für genau x Erfolge bei einer diskreten Binomialverteilung mit einer anzugebenden Anzahl der Stufen n (numtrials) und einer Erfolgswahrscheinlichkeit p. x ist eine nichtnegative ganze Zahl und kann mit den Optionen SINGLE (einzelner Wert), LIST (Liste) oder ALL (Liste aller Wahrscheinlichkeiten von 0 bis numtrials) eingegeben werden. 0 { p { 1 muss wahr sein. Die Wahrscheinlichkeitsdichtefunktion () lautet:
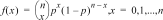
|
|
5:Binomialcdf
|
Berechnet die kumulierte Wahrscheinlichkeit für genau x Erfolge bei einer diskreten Binomialverteilung mit einer anzugebenden Anzahl der Stufen n (numtrials) und einer Erfolgswahrscheinlichkeit p. x kann eine nichtnegative ganze Zahl sein und mit den Optionen SINGLE (einzelner Wert), LIST (Liste) oder ALL (Liste aller kumulierten Wahrscheinlichkeiten) eingegeben werden. 0 { p { 1 muss wahr sein.
|
|
6:Poissonpdf
|
Berechnet die Wahrscheinlichkeit für x Erfolge für die diskrete Poisson-Verteilung mit dem angegebenen Mittelwert mu (m), bei dem es sich um eine reelle Zahl > 0 handeln muss. x kann eine nichtnegative ganze Zahl (SINGLE) oder eine Liste ganzer Zahlen (LIST) sein. Der Standardwert ist mu=1. Die Wahrscheinlichkeitsdichtefunktion () lautet:
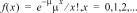
|
|
7:Poissoncdf
|
Berechnet die kumulierte Wahrscheinlichkeit für x Erfolge für die diskrete Poisson-Verteilung mit dem angegebenen Mittelwert mu, bei dem es sich um eine reelle Zahl > 0 handeln muss. x kann eine nichtnegative ganze Zahl (SINGLE) oder eine Liste ganzer Zahlen (LIST) sein. Der Standardwert ist mu=1.
|
Statistikergebnisse
|
|
1-Var
|
Anzahl von x oder (x,y) Datenpunkten
|
|
v
|
Beide
|
Mittelwert aller x-Werte
|
|
w
|
2-Var
|
Mittelwert aller y-Werte
|
|
|
Beide
|
Stichproben-Standardabweichung von x
|
|
|
2-Var
|
Stichproben-Standardabweichung von y
|
|
s
|
Beide
|
Standardabweichung der Grundgesamtheit von x
|
|
s
|
2-Var
|
Standardabweichung der Grundgesamtheit von y
|
|
G oder G2
|
Beide
|
Summe aller x- oder x2-Werte
|
|
G oder G2
|
2-Var
|
Summe aller y- oder y2-Werte
|
|
G
|
2-Var
|
Summe von (xQy) für alle xy-Paare
|
|
|
2-Var
|
Steigung der linearen Regression
|
|
|
2-Var
|
y-Achsenabschnitt der linearen Regression
|
|
2 oder
|
2-Var
|
Korrelationskoeffizient
|
|
¢
|
2-Var
|
Ermittelt bei Eingabe eines y-Werts anhand von a und b den voraussichtlichen x-Wert.
|
|
¢
|
2-Var
|
Ermittelt bei Eingabe eines x-Werts anhand von a und b den voraussichtlichen y-Wert.
|
|
oder
|
Beide
|
Minimum oder Maximum der x-Werte
|
|
|
1-Var
|
Median der Elemente zwischen minX und Med (1. Quartil)
|
|
|
1-Var
|
Median aller Datenpunkte
|
|
|
1-Var
|
Median der Elemente zwischen Med und maxX (3. Quartil)
|
|
oder
|
2-Var
|
Minimum oder Maximum der y-Werte
|
So definieren Sie statistische Datenpunkte:
|
1.
|
Geben Sie in L1, L2 oder L3 Daten ein. (Siehe Abschnitt „Dateneditor“.) |
Hinweis: Bei den Häufigkeitswerten können auch Dezimalzahlen eingegeben werden. Dies ist nützlich, wenn Sie die Häufigkeiten als Prozentwerte oder als Anteile eingeben, die zusammen 1 ergeben. Die Standardabweichung Sx der Stichprobe ist in diesem Fall jedoch nicht definiert, und für den betreffenden Wert wird Sx=Error angezeigt. Alle anderen Statistikwerte werden ordnungsgemäß angezeigt.
|
2.
|
Drücken Sie % u. Wählen Sie oder und drücken Sie <. |
|
3.
|
Wählen Sie L1, L2 oder L3 sowie die Häufigkeit aus. |
|
4.
|
Drücken Sie <, um das Variablenmenü anzuzeigen. |
|
5.
|
Um Daten zu löschen, drücken Sie v v, wählen die zu löschende Liste aus und drücken <. |
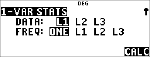
Beispiel für univariate Statistik
Finden Sie den Mittelwert von {45,55,55,55}.
|
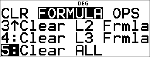
Alle Daten löschen
|
v v $ $ $
|
|
|
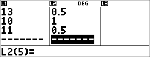
Daten
|
<
$ $ $
<
|

|
|
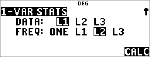
Statistik
|
% s
% u
|

|
|
|
(wählt )
$ $
|
|
|
|
<
|

|
|
Statistikvariable
|
<
|

|
|
|
V <
|

|
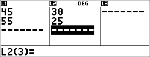
Beispiel für bivariate Statistik
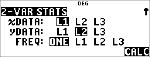
Daten: (45,30); (55,25). Ermitteln Sie: x¢(45).
|
Alle Daten löschen
|
v v $ $ $
|

|
|
Daten
|
< $ $ " $ $
|
|
|
Statistik
|
% u
|

|
|
|
(wählt )
$ $ $
|
|
|
StatVars
|
< % s
% u
# # # # # #
|
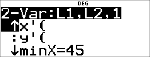
|
|
|
< ) <
|
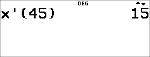
|
³ Aufgabe
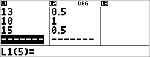
Rudi hat bei den letzten vier Klassenarbeiten die folgenden Noten bekommen. Die Arbeiten 2 und 4 werden jeweils mit 0,5 gewichtet, die Arbeiten 1 und 3 jeweils mit 1.
|
Arbeit
|
1
|
2
|
3
|
4
|
|
Punktzahl
|
12
|
13
|
10
|
11
|
|
Koeffizient
|
1
|
0,5
|
1
|
0,5
|
|
1.
|
Ermitteln Sie Rudis Durchschnittsnote (gewichteter Durchschnitt). |
|
2.
|
Wofür steht der vom Rechner ermittelte Wert n? Wofür steht der vom Rechner ermittelte Wert Gx? |
Zur Erinnerung: Der gewichtete Durchschnitt lautet
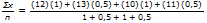
|
3.
|
Aus Versehen hat der Lehrer Rudi bei der vierten Arbeit vier Punkte zu wenig gegeben. Ermitteln Sie Rudis neue Durchschnittsnote. |
|
v v $ $ $
|

|
|
<
v " $ $ $ $
|
|
|
<
$ $ $ $
" $ $ $
<
|
|
|
% u
|

|
|
$ " " <
|
|
|
<
|
|
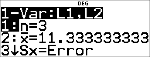
Rudis auf zwei Dezimalstellen gerundete Durchschnittsnote (v) ist 11,33.
Der vom Rechner angegebene Wert n steht für die Summe der Gewichtungsfaktoren.
n = 1 + 0,5 + 1 + 0,5.
Gx steht für die gewichtete Summe der Punktzahlen.
(12)(1) + (13)(0,5) + (10)(1) + (11)(0,5) = 34.
Ändern Sie Rudis letzte Note von 11 auf 15 Punkte.
|
v $ $ $ <
|
|
|
% u
$ " " < <
|

|
Wenn der Lehrer bei der vierten Arbeit vier Punkte mehr vergibt, hat Rudi einen Durchschnitt von 12 Punkten.
³ Aufgabe
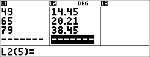
Die nachstehende Tabelle zeigt die Ergebnisse eines Bremstests.
|
Test Nr.
|
1
|
2
|
3
|
4
|
|
Geschwindigkeit (km/h)
|
33
|
49
|
65
|
79
|
|
Bremsweg (m)
|
5,30
|
14,45
|
20,21
|
38,45
|
Schätzen Sie anhand der Korrelation von Geschwindigkeit und Bremsweg den Bremsweg bei einer Geschwindigkeit von 55 km/h.
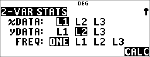
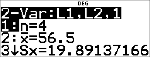
Ein von Hand gezeichnetes Streudiagramm der Daten lässt einen linearen Zusammenhang vermuten. Der Rechner ermittelt nach der Methode der kleinsten Quadrate die Ausgleichsgerade y'=ax'+b für die Daten aus den Listen.
|
v v $ $ $
|

|
|
<
$ $ $ $ " $ $ $ <
|
|
|
% s
% u
|

|
|
(wählt )
$ $ $
|
|
|
<
|
|
|
Blättern Sie mit $ zu a und b.
|
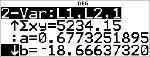
|
Die Ausgleichsgerade y'=0,67732519x'N18,66637321 modelliert einen linearen Zusammenhang der Daten.
|
Drücken Sie $, bis y' markiert ist.
|

|
|
< ) <
|

|
Für ein Fahrzeug mit einer Geschwindigkeit von 55 km/h ergibt das lineare Modell einen Bremsweg von 18,59 Meter.
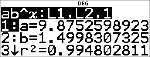
Regression – Beispiel 1
Berechnen Sie eine lineare Regression (ax+b) für die folgenden Daten: {1,2,3,4,5}; {5,8,11,14,17}.
|
Alle Daten löschen
|
v v $ $ $
|

|
|
Daten
|
<
$ $ $ $
$ "
$ $ $ $
<
|
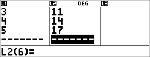
|
|
Regression
|
% s
% u
$ $ $
|

|
|
|
<
|
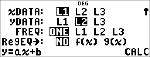
|
|
|
$ $ $ $
<
Drücken Sie $, um alle Ergebnisvariablen zu untersuchen.
|

|
Regression – Beispiel 2
Berechnen Sie eine exponentielle Regression für die folgenden Daten:
|
•
|
L1 = {0,1,2,3,4}; L2 = {10,14,23,35,48} |
|
•
|
Ermitteln Sie den Durchschnitt der Daten in L2. |
|
•
|
Vergleichen Sie die Werte der exponentiellen Regression mit L2. |
|
Alle Daten löschen
|
v v
|
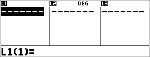
|
|
Daten
|
$ $ $ $
$ " $ $ $ $ <
|
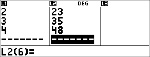
|
|
Regression
|
% u
# #
|
|
|
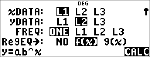
Speichern Sie die Regressionsgleichung
unter f(x) im Menü I.
|
< $ $ $ "
<
|
|
|
Regressionsgleichung
|
<
|
|
|
Ermitteln Sie über das Menü StatVars den Durchschnitt (y) der Daten in L2.
|
% u
(wählt )
$ $ $
$ $ $
$ $
|
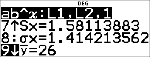
Beachten Sie, dass in der Titelleiste Ihre letzte Statistik- bzw. Regressionsberechnung angezeigt wird.
|
|
Untersuchen Sie die Wertetabelle der Regressionsgleichung.
|
I
|

|
|
|
< $
<
<
|

|
|
|
< <
|
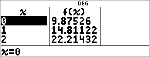
|
Warnung: Wenn Sie nun die bivariate Statistik (2-Var Stats) für Ihre Daten berechnen, werden die Variablen und (sowie und 2) auf Grundlage einer linearen Regression berechnet. Wenn nach einer Regressionsberechnung die Regressionskoeffizienten (a, b, c, d) und r-Werte im Menü erhalten bleiben sollen, sollten Sie anschließend also nie die bivariate Statistik neu berechnen.
Verteilung – Beispiel
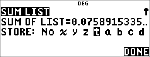
Berechnen Sie die Wahrscheinlichkeit für x {3,6,9} Erfolge bei einer Binomialverteilung mit 20 Versuchen und einer Erfolgswahrscheinlichkeit von 0,6. Geben Sie die x-Werte in der Liste L1 ein, speichern Sie die Ergebnisse in L2 und ermitteln Sie anschließend die Summe der Wahrscheinlichkeiten und speichern Sie sie in der Variablen t.
|
Alle Daten löschen
|
v v $ $ $
|

|
|
Daten
|
<
$ $
<
|
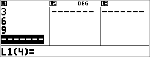
|
|
DISTR
|
% u "
$ $ $
|

|
|
|
< "
|
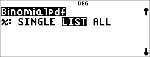
|
|
|
<
$
|
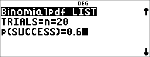
|
|
|
< $ $
|
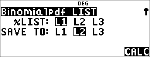
|
|
|
<
|
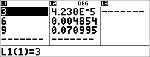
|
|
|
v ! "
<
|
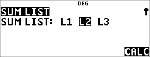
|
|
|
<
" " " "
< <
|
|