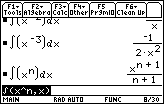
Because
![]() ,
,
![]() and
and
![]() , it appears that the exponent of x in the antiderivative is one greater than the exponent of the original function and that the antiderivative is divided by the value of its exponent. Predict that
, it appears that the exponent of x in the antiderivative is one greater than the exponent of the original function and that the antiderivative is divided by the value of its exponent. Predict that
![]() is
is
![]() .
.


The TI-89 results may appear to be different from your predictions, however they are algebraically equivalent to
![]() and
and
![]() , respectively.
, respectively.
|
|||
|
|
|||
![]()
then
![]()
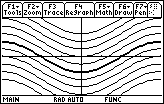
The family of curves
![]() is shown in a [-4
is shown in a [-4
![]() , 4
, 4
![]() ] x [-10, 10] window with
] x [-10, 10] window with
C = -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, and 10. The curve with C = 0 is darker.
![]()
The general solution is y = Cex .
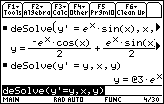

The solution to y' = 2x with y(2)=1 is y = x2 – 3.

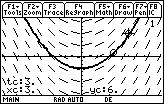
y(3) = 6
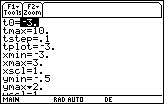

Enter y1' = y1, not y1' = y, be sure to clear yi1, and use a [-3, 3] x [-5, 10] window.


Instead of parallel line segments in columns, line segments in rows are parallel.
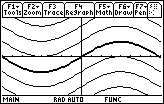
The indefinite integral
![]() , displayed in a [-2
, displayed in a [-2
![]() , 2
, 2
![]() ] x [-5, 5] window, with C = -6, -4, -2, 0, 2, 4, 6.
] x [-5, 5] window, with C = -6, -4, -2, 0, 2, 4, 6.
![]()
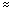 3.29584
3.29584
![]()
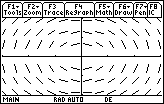
[-3, 3] x [-2, 2]
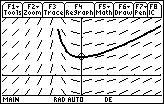
[-3, 3] x [-1, 3]
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy