| Rectangle | x-coordinate | y-coordinate | Width | Height | Area |
| 1 | 1/4 | 1/16 | 1/4 | 1/16 | 1/64 |
| 2 | 1/2 | 1/4 | 1/4 | 1/4 | 1/16 |
| 3 | 3/4 | 9/16 | 1/4 | 9/16 | 9/64 |
| 4 | 1 | 1 | 1/4 | 1 | 1/4 |
| Total | 15/32 |
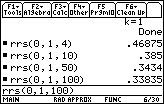
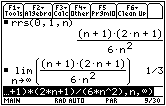
We can read that
![]()
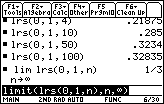
The area under f(x) = x2 and above the x-axis between x = 0 and x = 1 is
![]() square unit.
square unit.
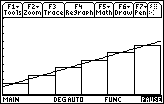
The graph illustrating the midpoint rectangles is at left below and the approximate areas found using different types of rectangles is shown at right.
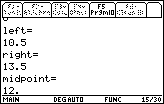

In the screen shown, the value of
![]() was found by two methods using the definite integral key. In the first, the function g was defined and then the definite integral was evaluated with its name. In the second, the expression that defines the function was entered directly. In both cases, the area under the graph of g(x) = 2x + 1 and above the x-axis between x = 0 and x = 3 is 12 square units.
was found by two methods using the definite integral key. In the first, the function g was defined and then the definite integral was evaluated with its name. In the second, the expression that defines the function was entered directly. In both cases, the area under the graph of g(x) = 2x + 1 and above the x-axis between x = 0 and x = 3 is 12 square units.
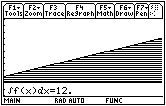
The area under the curve g(x) = 2x + 1 between x = 0 and x = 3 is 12.
0.3025
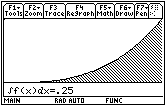
0.2025
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy