Module 14 - Related Rates

Module 14 - Answers

Lesson 1

Answer 1

14.1.1 The bottom of the ladder moves at a constant rate of 3 ft/sec while the top of the ladder falls at an increasing rate.

Answer 2

14.1.2

. The negative sign indicates that y is decreasing.

Answer 3

14.1.3 The velocity of the ladder's top is given by

Answer 4

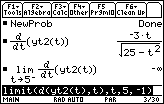
14.1.4 Solving yt2(t)=0 indicates that the top of the ladder hits the ground after 5 seconds, but

is undefined at that time. As t approaches 5 seconds,

grows without bound. So in theory the top is going infinitely fast when it hits the ground as suggested by the following figure.

Lesson 2

Answer 1

14.2.1 The parametric equations that model the ladder's position at time t are shown in the screen below.

Answer 2

14.2.2 The top of the ladder is falling at an increasing rate while the bottom is moving at a decreasing rate.

Answer 3

14.2.3 Using the derivative of the position of the bottom of the ladder, xt2(t), and evaluating it at the given times, the bottom is moving at approximately 21.2015 ft/sec, 17.2582 ft/sec, and 8.5665 ft/sec, respectively.

Lesson 3

Answer 1

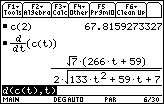
14.3.1 About 61.0 nautical miles.

Answer 2

14.3.2

Self Test

Answer 1

x(t) = 0

y(t) = 15 – 45t

Answer 2

x(t) = 24 – 52t

y(t) = 0

Answer 3

The car coming from the North will arrive at the intersection first.

Answer 4

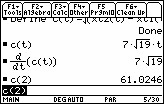
Define

Answer 5

with t = 0.25 is approximately -63.739, so the distance between the cars is decreasing at a rate of 63.739 mph.