|
Module 12 - Answers
|
|
|
|
Lesson 1
|
|
|
|
Answer 1
|
|
|
|
12.1.1
The particle is moving to the right when 0 < t < 1 and when 2 < t < 4. If you increase the value of tmax you will see that the particle appears to be moving to the right for t > 2.
|
|
|

|

|
|
Answer 2
|
|
|
|
12.1.2
The particle is moving to the left when 1 < t < 2.
|
|
|

|

|
|
Answer 3
|
|
|
|
12.1.3
The particle appears to change direction at t = 1 and t = 2.
|
|
|

|

|
|
Answer 4
|
|
|
|
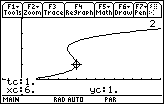
12.1.4
The turning points correspond to the times when the particle appears to change direction.
|
|
|

|

|
|
Answer 5
|
|
|
|
12.1.5
The graph of the velocity is a parabola. When the velocity is positive, the particle is moving to the right. When the velocity is negative, the particle is moving to the left. When the particle is at rest, the velocity is zero. When the position graph is increasing, the particle is moving to the right. When it's decreasing, the particle is moving to the left. At the local extreme (and in general at the location of any horizontal tangent line), the particle is at rest.
|
|
|

|

|
|
Lesson 2
|
|
|
|
Answer 1
|
|
|
|
12.2.1
A smaller value of tstep slows the motion of the ball because more values of t are used in calculating and plotting its motion.
|
|
|

|

|
|
Answer 2
|
|
|
|
12.2.2
The particle is moving upward when 0 < t < 0.75 and when 2.25 < t < 3.75.
|
|
|

|

|
|
Answer 3
|
|
|
|
12.2.3
The particle is moving downward when 0.75 < t < 2.25 and when 3.75 < t < 5.
|
|
|

|

|
|
Answer 4
|
|
|
|
12.2.4
The particle is at rest at t = 0.75, t = 2.25, and t = 3.75
|
|
|

|

|
|
Answer 5
|
|
|
|
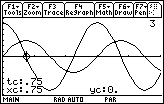
12.2.5
The first time the particle is at rest is at t = 0.75, as shown below.
|
|
|

|

|
|
Answer 6
|
|
|
|
12.2.6
When the derivative is negative the particle is moving downward. When the derivative is positive the particle is moving upward.
|
|
|

|

|
|
Lesson 3
|
|
|
|
Answer 1
|
|
|
|
12.3.1
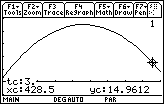
Because the ball is more than 14 feet high when it is 428 feet away, it clears the fence.
|
|
|

|

|
|
Answer 2
|
|
|
|
12.3.2
The maximum height reached by the ball is approximately 45.229 feet.
|
|
|

|

|
|
Answer 3
|
|
|
|
12.3.3
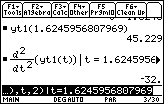
Because the second derivative is negative at the critical point t
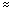 1.6246, the value of yt1 is a local maximum. In this case it is also the absolute maximum.
1.6246, the value of yt1 is a local maximum. In this case it is also the absolute maximum.
|
|
|

|

|
|
Self Test
|
|
|
|
Answer 1
|
|
|
x(t) = t3 – 11t2 + 38t – 30
y(t) = 0
Graph Style: 5:Animate
|
|
|
|
Answer 2
|
|
|
x(t) = t3 – 11t2 + 38t – 30
y(t) = t
Graph Style: 6:Path
|
|
|
|
Answer 3
|
|
|
|
The leftmost position of the particle is –30.
|
|
|
|
Answer 4
|
|
|
|
The particle is moving to the right approximately when 0 < t < 2.8 and when 4.5 < t < 7.
|
|
|
|
Answer 5
|
|
|
|
The particle is moving to the left approximately when 2.8 < t < 4.5.
|
|
|
|
Answer 6
|
|
|
|
The particle is at rest at approximately t = 2.8 and t = 4.5 seconds.
|
|
|
|
Answer 7
|
|
|
x(t) = 138tcos(30)
y(t) = –16t2 + 138tsin(30) + 3.5
|
|
|
|
Answer 8
|
|
|
|
The ball will hit the ground about 4.36 seconds after it was struck and about 521 feet away from home plate.
|
|
|
|
Answer 9
|
|
|
|
The height of the ball is an inverted parabola, so the maximum height occurs where the derivative of yt1(t) is zero. The maximum height of the ball is approximately 77.89 ft. This value occurs at t = 2.15625 = 69/32.
|
|
|

|
©Copyright
2007 All rights reserved. |
Trademarks
|
Privacy Policy
|
Link Policy
|




![]() 1.6246, the value of yt1 is a local maximum. In this case it is also the absolute maximum.
1.6246, the value of yt1 is a local maximum. In this case it is also the absolute maximum.