Module 10 - Rules of Differentiation

Module 10 - Answers

Lesson 1

Answer 1

10.1.1

Answer 2

10.1.2 The exponent in the function becomes the coefficient of the derivative and the exponent of the derivative is one less than the exponent in the function.

Answer 3

10.1.3 Predict that

and

, which are verified in the screen below.

Answer 4

10.1.4 Generalize that

, which is verified in the screen below.

Answer 5

10.1.5

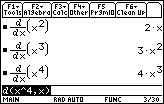
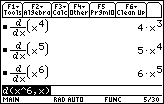
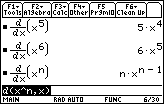
The Power Rule appears to be valid for other types of exponents.

Lesson 2

Answer 1

10.2.1

Answer 2

10.2.2 Predict that

, which is verified below.

Answer 3

10.2.3 Predict that

Answer 4

10.2.4

Answer 5

10.2.5 Predict

, which is equivalent to the expression shown in the screen below.

Answer 6

10.2.6 Predict that

and that

, which are each respectively equivalent to the expressions shown below.

Answer 7

10.2.7 The derivative of the product of two functions f and g is given by

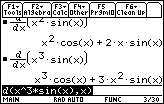
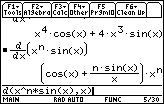
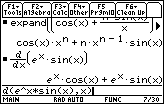
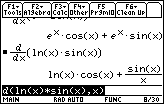
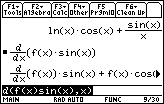
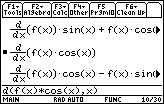
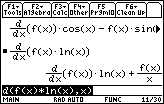
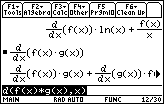
You will have to scroll to the right in the History Area to see the entire result of , which is equivalent to the one stated in the theorem.

Lesson 4

Answer 1

10.4.1

This result is known as the Chain Rule for derivatives.

Self Test

Answer 1

Answer 2

Answer 3

Answer 4

2:Save Copy As... in the F1:Tools menu

Answer 5

8:Text Editor in the APPs menu, then select 2:open...

Answer 6

To find the derivative of a cofunction, negate the derivative of the original function and replace the functions in the derivative with their cofunctions.