
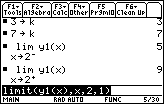
It may be faster to copy and paste the previous commands from the History Window to the Edit Line and change
![]() to 0.
to 0.
Although
![]() exists, f(0) is undefined. Therefore,
exists, f(0) is undefined. Therefore,
![]() is not continuous at x = 0.
is not continuous at x = 0.

The function will be continuous if these limits are equal. Setting 2 + k = 5 gives k = 3. So if k = 3,
![]() and the function is continuous.
and the function is continuous.
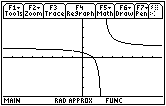
The window shown is [–7.9, 7.9] x [–3.8, 3.8] (ZoomDec) with xres = 1.
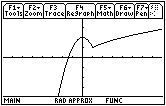
The window shown is [–7.9, 7.9] x [–3.8, 3.8] (ZoomDec)
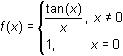
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy