The coefficient of x in the equation of the tangent line is the value of the derivative at the point of tangency because the derivative is the slope of the tangent line.

- The derivative is negative on the interval where the function is decreasing.
- The derivative is positive on the intervals where the function is increasing.
![]()
The slopes steadily increase until about x = 0.7 after which the slopes decrease. The screen below is the last screen displayed after running tanimate. The points on the dotted curve represent the slopes of the tangent lines at the corresponding x-values.

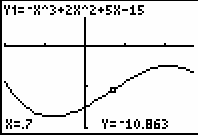
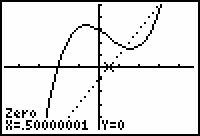
The inflection point occurs when
![]() .
.
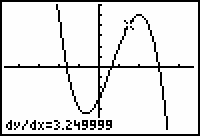
The derivative of the function at x = 1.5 is
![]() .
.
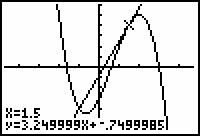
The equation of the tangent line to the curve at x = 1.5 is y = 3.25x - 0.75.
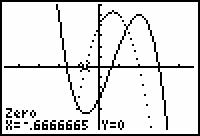
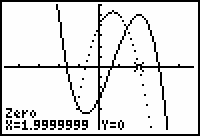
The turning points of the function occur when x
![]() -2/3 and x
-2/3 and x
![]() 2.
2.
The function is increasing on (-0.667, 2) and decreasing on
![]() and
and
![]() .
.
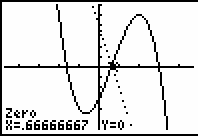
The inflection point occurs when
![]() .
.
The function is concave upward on
![]() and concave downward on
and concave downward on
![]() .
.
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy