Voorbeeld: U kunt een kansverdeling berekenen die past op het model van de Normale Pdf-verdeling.
| 1. | Voer de X-waarden van de gegevens in in kolom A. |
| 2. | Tik op de bovenste cel van kolom A en voer een naam in, zoals DD1, voor de X-waarden. |
| 3. | Tik op de kolomformulecel (tweede cel van boven) in kolom B. |
| 4. | Tik op Hulpmiddelen  en ga naar Statistiek > Verdelingen > Normale Pdf. en ga naar Statistiek > Verdelingen > Normale Pdf. |
Het dialoogvenster Normale Pdf wordt geopend en er worden velden weergegeven voor het invoeren van de argumenten voor de berekening.
| 5. | Tik op elk veld en geef: |
| - | X-waarde: Om de lijst te gebruiken die u hebt gedefinieerd in stap 2, tikt u op het pijltje en selecteert u de naam van de lijst. |
| - | Gemiddelde (μ): Typ een waarde of selecteer een variabele die het gemiddelde bevat. |
| - | Standaarddeviatie (σ): Typ een waarde of selecteer een variabele die de standaarddeviatie bevat. |
| 6. | (Optioneel) Selecteer de optie Tekenen om de verdeling te plotten in Gegevensverwerking & Statistiek. |
Opmerking: de optie Tekenen is niet beschikbaar bij alle verdelingen.
| 7. | Tik op OK. |
Lijsten & Spreadsheet vult kolom B met de resultaten. De resultaten worden geplot in Gegevensverwerking & Statistiek.
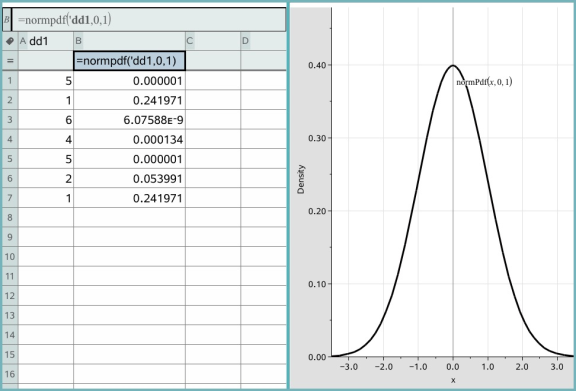
Opmerking: de resultaten zijn gekoppeld aan de brongegevens. Als u bijvoorbeeld een waarde in kolom A verandert, wordt het resultaat automatisch bijgewerkt.
In de toepassing Lijsten & Spreadsheet zijn de volgende verdelingen beschikbaar. Zie voor meer informatie over deze functies de Handleiding over TI-Nspire™.
| • | Om een enkel verdelingsresultaat te verkrijgen op basis van een enkele waarde typt u de functie in een enkele cel. |
| • | Om een lijst verdelingsresultaten te verkrijgen op basis van een lijst waarden typt u de functie in een kolomformulecel. In dit geval geeft u een lijst (kolom) op die de waarden bevat. Voor iedere waarde in de lijst geeft de verdeling een overeenkomstig resultaat. |
Opmerking: Voor kansverdelingsfuncties die de tekenoptie ondersteunen (normPDF, t PDF, χ² Pdf, en F Pdf), is deze optie alleen beschikbaar als u de verdelingsfunctie in een formulecel typt.
Normale Pdf (normPdf)
Berekent de kansdichtheidsfunctie (pdf) voor de normale verdeling bij een gespecificeerde x-waarde. De standaardwaarden zijn: gemiddelde μ=0 en standaardafwijking σ=1. De kansdichtheidsfunctie (pdf) is:
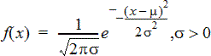
Deze verdeling wordt gebruikt om de kans dat een bepaalde waarde voorkomt in een normale verdeling te bepalen. De tekenoptie is beschikbaar wanneer Normal PDF wordt opgeroepen vanuit een formulecel.
Wanneer u verdelingen opent vanuit de formulecel, moet u een geldige lijst uit de keuzelijst selecteren om onverwachte resultaten te voorkomen. Als u de verdeling opent vanuit een cel moet u een getal opgeven voor de x-waarde. De verdeling geeft de kans dat de waarde die u opgeeft, voorkomt.
Normale Cdf (normCdf)
Berekent de kans bij de normale verdeling tussen de ondergrens en de bovengrens voor het gespecificeerde gemiddelde, μ (standaard=0) en de standaarddeviatie, s (standaard=1). U kunt op het vakje Tekenen (Oppervlakte arceren) klikken om de oppervlakte tussen de onder- en bovengrenzen te arceren. Bij veranderingen in de oorspronkelijke ondergrens en bovengrens wordt de verdeling automatisch bijgewerkt.
Deze cumulatieve verdeling wordt gebruikt voor het bepalen van de kans op een waarde tussen de onder- en bovengrens in de normale verdeling. Dit is hetzelfde als het vinden van de oppervlakte onder de gespecificeerde normale kromme tussen de grenzen.
Inverse-normaal (invNorm)
Berekent de inverse cumulatieve normale verdelingsfunctie voor een gegeven oppervlakte onder de normale verdelingskromme, die gespecificeerd wordt door gemiddelde, μ, en standaarddeviatie, s.
Deze verdeling wordt gebruikt voor het bepalen van de x-waarde van de gegevens in het gebied van 0 tot x<1 wanneer het percentiel bekend is.
t Pdf (tPdf)
Berekent de kansdichtheidsfunctie (pdf) voor de t--verdeling bij een gespecificeerde x-waarde. df (aantal vrijheidsgraden) moet > 0 zijn. De kansdichtheidsfunctie (pdf) is:
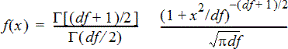
Deze verdeling wordt gebruikt voor het bepalen van de kans op een waarde, wanneer de standaarddeviatie van de populatie niet bekend is en de steekproefomvang klein is. De tekenoptie is beschikbaar wanneer t Pdf wordt opgeroepen vanuit een formulecel.
t Cdf (tCdf)
Berekent de kans bij de Student-t-verdeling tussen ondergrens en bovengrens bij de gespecificeerde df (aantal vrijheidsgraden). U kunt op het vakje Tekenen (Oppervlakte arceren) klikken om de oppervlakte tussen de grenzen te arceren. Bij veranderingen in de oorspronkelijke ondergrens en bovengrens wordt de verdeling automatisch bijgewerkt.
Deze cumulatieve verdeling wordt gebruikt voor het bepalen van de kans op een waarde binnen een interval dat gedefinieerd wordt door de onder- en bovengrens voor een normaal verdeelde populatie wanneer de populatiestandaarddeviatie niet bekend is.
Inverse t (invt)
Berekent de inverse cumulatieve t-kansverdelingsfunctie die gespecificeerd wordt door het aantal vrijheidsgraden, df, voor een gegeven oppervlakte onder de kromme.
Deze verdeling wordt gebruikt voor het bepalen van de kans dat er gegevens voorkomen in het gebied van 0 tot x<1. Deze functie wordt gebruikt wanneer het gemiddelde en/of de standaardafwijking van de populatie niet bekend zijn.
c2 Pdf (c2 Pdf())
Berekent de kansdichtheidsfunctie (pdf) voor de c2 (chi-kwadraat) verdeling bij een gespecificeerde x-waarde. df (aantal vrijheidsgraden) moet een geheel getal > 0 zijn. De kansdichtheidsfunctie (pdf) is:
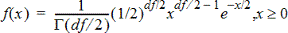
Deze verdeling wordt gebruikt voor het bepalen van de kans op een gegeven waarde uit een populatie met een c2-verdeling. De tekenoptie is beschikbaar wanneer c2Pdf wordt opgeroepen vanuit een formulecel.
c2 Cdf (c2 Cdf())
Berekent de kans voor de c2 (chi-kwadraat) verdeling tussen ondergrens en bovengrens voor de gespecificeerde df (aantal vrijheidsgraden). U kunt het vakje Tekenen (Oppervlakte arceren) aanklikken om de oppervlakte tussen de onder- en bovengrenzen te arceren. Veranderingen in de oorspronkelijke ondergrens en bovengrens werken de verdeling automatisch bij.
Deze verdeling wordt gebruikt voor het bepalen van de kans op een waarde binnen gegeven grenzen van een populatie met een c2-verdeling.
F Pdf (F Pdf())
Berekent de kansdichtheidsfunctie (pdf) voor de F-verdeling bij een gespecificeerde x-waarde. De teller df (aantal vrijheidsgraden) en noemer df moeten gehele getallen > 0 zijn. De kansdichtheidsfunctie (pdf) is:
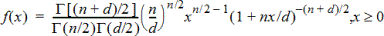
|
waarbij |
n = teller vrijheidsgraden |
Deze verdeling wordt gebruikt voor het bepalen van de kans dat twee steekproeven dezelfde variantie hebben. De tekenoptie is beschikbaar wanneer F Pdf wordt opgeroepen vanuit een formulecel.
F Cdf (F Cdf())
Berekent de kans voor de F-verdeling tussen ondergrens en bovengrens voor de gespecificeerde dfTeller (aantal vrijheidsgraden) en dfNoemer. U kunt op het vakje Tekenen (Oppervlakte arceren) klikken om de oppervlakte tussen de onder- en bovengrenzen te arceren. Bij veranderingen in de oorspronkelijke ondergrens en bovengrens wordt de verdeling automatisch bijgewerkt.
Deze verdeling wordt gebruikt voor het bepalen van de kans dat een enkele observatie binnen het bereik tussen de ondergrens en de bovengrens valt.
Binomiale Pdf (binomPdf())
Berekent de kans op x voor de discrete binomiale verdeling met het gespecificeerde AantalPogingen en de succeskans (p) bij elke poging. De x-parameter kan een geheel getal of een lijst met gehele getallen zijn. 0{p{1 moet waar zijn. AantalPogingen moet een geheel getal > 0 zijn. Als u x niet specificeert, wordt er een lijst met kansen van 0 tot aantalPogingen gegeven. De kansdichtheidsfunctie (pdf) is:
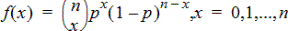
waarbij n = aantalPogingen
Deze verdeling wordt gebruikt voor het bepalen van de kans op succes bij den-de poging in een succes-/geen-succes experiment. U kunt deze verdeling bijvoorbeeld gebruiken om bij het gooien van kop of munt de kans op kop te voorspellen bij de vijfde keer opgooien.
Binomiale Cdf (binomCdf())
Berekent de cumulatieve kans voor de discrete binomiale verdeling met aantal pogingen n en succeskans p bij iedere poging.
Deze verdeling wordt gebruikt voor het bepalen van de kans op succes bij één poging, voordat alle pogingen voltooid zijn. Als bijvoorbeeld kop een succesvol resultaat is en u wilt de munt 10 maal opgooien, dan voorspelt deze verdeling de kans op minimaal één maal kop in de 10 worpen.
Inverse binomiaal (invBinom())
Gezien het aantal pogingen (AantalPogingen) en de kans op succes van elke poging (Kans), geeft deze functie het minimum aantal successen, k, zodanig dat de waarde, k, groter is dan of gelijk aan de gegeven cumulatieve kans (CumulatieveKans).
Deze verdeling wordt gebruikt bij het bepalen van de invoer voor de bovengrens van de binomiale cdf. Bijvoorbeeld, als u 10 keer een munt opgooit, en u wilt dat de kans om x keer of minder kop te krijgen meer dan 75% bedraagt, dan zal deze distributie helpen te bepalen wat x zou moeten zijn.
Inverse binomiaal ten opzichte van N (invBinomN())
Gezien de kans op succes voor elke poging (Kans) en het aantal successen van elke poging (AantalSucces), geeft deze functie het minimum aantal pogingen, N, zodanig dat de waarde, N, lager is dan of gelijk aan de gegeven cumulatieve kans (CumulatieveKans).
Deze verdeling wordt gebruikt bij het bepalen van het aantal pogingen van de binomiale cdf. Bijvoorbeeld, als u een aantal keren een munt opgooit, en u wilt dat de kans om 6 keer of minder een kop te krijgen minder dan 25% bedraagt, dan zal deze distributie helpen te bepalen hoe vaak de munt opgegooid moet worden.
Poisson verdeling (poissPdf()
Berekent de kans bij x voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde, μ, dat een reëel getal > 0 moet zijn. x kan een geheel getal of een lijst met gehele getallen zijn. De kansdichtheidsfunctie (pdf) is:
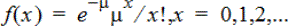
Deze verdeling wordt gebruikt voor het bepalen van de kans op een bepaald aantal successen voordat een experiment begint. U kunt deze berekening bijvoorbeeld gebruiken om het aantal malen kop te voorspellen dat zou optreden bij achtmaal opgooien van een munt.
Cumulatieve Poisson verdeling (poissCdf())
Berekent een cumulatieve kans voor de discrete Poisson-verdeling met het gespecificeerde gemiddelde x.
Deze verdeling wordt gebruikt voor het bepalen van de kans dat een bepaald aantal successen optreedt tussen de boven- en ondergrenzen van een poging. U kunt deze berekening bijvoorbeeld gebruiken om het aantal malen kop te voorspellen dat voorkomt tussen worp #3 en worp #8 van de munt.
Geometrische Pdf (geomPdf())
Berekent de kans op x, het nummer van de poging waarbij het eerste succes optreedt, voor de discrete geometrische verdeling met de gespecificeerde succeskans p. 0{p{1 moet waar zijn. x kan een geheel getal of een lijst met gehele getallen zijn. De kansdichtheidsfunctie (pdf) is:
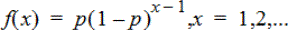
Deze verdeling wordt gebruikt voor het bepalen van het meest waarschijnlijke aantal pogingen voordat er een succes optreedt. U kunt deze berekening bijvoorbeeld gebruiken om het aantal worpen met een muntstuk te voorspellen dat uitgevoerd moet worden voordat u kop krijgt.
Cumulatieve Geometrische verdeling (geomCdf())
Berekent een cumulatieve geometrische kans van ondergrens tot bovengrens met de gespecificeerde succeskans p.
Deze verdeling wordt gebruikt voor het bepalen van de kans die bij het eerste succes hoort dat optreedt tussen de pogingen 1 enn. U kunt deze berekening bijvoorbeeld gebruiken om de kans te voorspellen dat u kop krijgt bij de worpen #1, #2, #3, ..., #n.