In this lesson you will study several power series and discover that on the intervals where they converge, they are equal to certain well known functions.

Defining Power Series

A power series is a series in which each term is a constant times a power of x or a power of (x - a).

Suppose each c_k represents some constant.

The infinite series

is a power series centered at x = 0.

The infinite series

is a power series centered at x = a.

Finding Partial Sums of a Power Series

Consider the power series

Although you cannot enter infinitely many terms of this series in the Y= Editor, you can graph partial sums of the series because each partial sum is a polynomial with a finite number of terms.

Graphing Partial Sums of a Power Series

• Set Graph mode to FUNCTION

22.1.1 Graph the second, third and fourth partial sums of the power series in a [-5, 5] x
[-10, 10] window. On what interval do the graphs appear to coincide?
Click here for the answer.

Defining an Infinite Geometric Series

Recall that an infinite geometric series can be written as a + ar + ar² + ar³ + ... + ar^k + ..., where a represents the first term and r represents the common ratio of the series.

If | r | < 1, the infinite geometric series a + ar + ar² + ar³ + ... + ar^k + ... converges to .

The power series

is a geometric series with first term 1 and common ratio x. This means that the power series converges when | x | < 1 and converges to on the interval (-1, 1).

Visualizing Convergence

The graphs of several partial sums can illustrate the interval of convergence for an infinite series.

• Graph 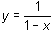along with the second-, third- and fourth-degree polynomials that represent partial sums of .
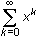• Change the graphing style for 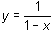to "thick" to distinguish it from the partial sums

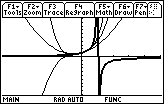
On the interval (-1,1) the partial sums are close to . The interval (-1,1) is called the interval of convergence for this power series. As the number of terms in the partial sums increase, the partial sums converge to .

22.1.2 Graph the tenth-degree partial sum of y = 1/(1 - x) in a [-2, 2] x [-2, 8] viewing window. Use the
" (" command to enter the partial sum. Click here for the answer.

Investigating Another Power Series

Consider the power series

• Graph the seventh-, eleventh- and fifteenth-degree polynomial partial sums in a
  [-10, 10] x [-2, 2] window

Using Previously Defined Graphing Variables You don't have to enter every term of each partial sum. Enter the expressions below in the Y= Editor by typing y1(x) and y2(x). y1 = x - x^3/3! + x^5/5! - x^7/7! y2 = y1(x) + x^9/9! - x^11/11! y3 = y2(x) + x^13/13! - x^15/15! Recall that the ! symbol can be obtained by pressing .

22.1.3 Examine the graphs of the partial sums listed above on the interval -6 < x < 6. The partial sums seem to converge to what familiar function?
Click here for the answer.

22.1.4 For the partial sums in Question 22.1.2 graph the familiar function along with the partial sums in a [-10, 10] x [-2, 2] window. Change the graphing style of the familiar function to "thick".
Click here for the answer.

Adding More Terms to Partial Sums

As more terms are added to form successive partial sums, more turning points appear in each successive graph and the power series converges to the function y = sin x on the interval (– , ).

Illustrating Convergence of

In Lesson 22.2 you will see that the power series

converges to e^x.

Graphing the second-, fifth-, eighth- and eleventh-degree partial sums of the power series illustrates that the infinite series converges to y = e^x.

• Set y1= e^x and its graphing style to "thick"
• Enter the desired partial sums of 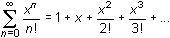into y2, y3, y4 and y5, respectively

  Use the short cut that was described in the Tech Tip for the previous power series to enter the partial sums.

• Try several different windows.

22.1.5 What seems to happen to the interval where the partial sums are approximately equal to e^x as more terms are added in successive partial sums?
Click here for the answer.