In this lesson you will find the area of the region bounded by the graph of f(x) = x2, the vertical line

Getting a First Approximation
Adding the areas of the four rectangles shown below can approximate the area under the curve. The rectangles are called right-hand rectangles because the upper-right-hand corner of each lies on the graph of f(x) = x2.
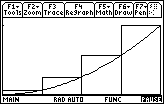
Finding the Width of Each Rectangle
The rectangles have equal widths along the x-axis that can be found by dividing the length of the interval by the number of rectangles. Using four rectangles over the interval [0, 1], the width of each rectangle shown is
![]() .
.
The x-coordinate of each right-hand endpoint is found by repeatedly adding the fixed width,
![]() , to the beginning point of the interval. In the example under discussion the four right-hand endpoints are
, to the beginning point of the interval. In the example under discussion the four right-hand endpoints are
![]() and 1.
and 1.
Finding the Area
Because the upper-right-hand corner of each rectangle is on the curve, the height of each rectangle is determined by the function, and the heights are found by evaluating the function at the right-hand x-coordinates. For example, the x-coordinate at the right-hand edge of the third rectangle is
![]() and its height is
and its height is
![]() .
.
The area of each rectangle is found by multiplying the rectangle's width times the corresponding height. The total area under the curve is approximated by the sum of the areas of all the rectangles.
15.1.1 Approximate the area under the curve f(x) = x2 between x = 0 and x = 1 using four right-hand rectangles by completing the table below. Enter the right-hand x-coordinate and the corresponding y-coordinate for each rectangle, find each rectangle's width and height, and enter its area.
| Rectangle | x-coordinate | y-coordinate | Width | Height | Area |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| Total |
Click here for the answer.
Finding a Better Approximation
To find a better approximation you could subdivide the region into more rectangles, but it is more instructive to find a general procedure using an unspecified number of rectangles. The following table shows how to find the sum of n rectangular areas.
Using n Rectangles
Let x = a be the left side of the region, let x = b be the right side of the region, and let f represent the function. The width of each of the n rectangles is given by
![]() and each right-hand x-coordinate is found by adding multiples of w to a, the left endpoint of the interval. The y-coordinate at the upper-right-hand corner of the rectangle (height) is found by evaluating the function at the corresponding x-value.
and each right-hand x-coordinate is found by adding multiples of w to a, the left endpoint of the interval. The y-coordinate at the upper-right-hand corner of the rectangle (height) is found by evaluating the function at the corresponding x-value.
Study the table carefully. It will help you understand how to define an expression for finding the area of a general rectangle that will be used to find the sum of the rectangular areas.
| Rectangle | x-coordinate | y-coordinate | Width | Height | Area |
| 1 | a + w | f(a + w) | w | f(a + w) | w * f(a + w) |
| 2 | a + 2w | f(a + 2w) | w | f(a + 2w) | w * f(a + 2w) |
| 3 | a + 3w | f(a + 3w) | w | f(a + 3w) | w * f(a + 3w) |
| ... | ... | ... | ... | ... | ... |
| k | a + kw | f(a + kw) | w | f(a + kw) | w * f(a + kw) |
| ... | ... | ... | ... | ... | ... |
| n | a + nw | f(a + nw) | w | f(a + nw) | w * f(a + nw) |
| Total |
|
Creating the Right-hand Area Function
As shown in the previous table, each right-hand x-coordinate has the form a + kw, where k = 1, 2, 3, ..., n. The height of the corresponding rectangle has the form f(a + kw), and the area of the region is approximated by adding the areas of the rectangles, which is expressed as
![]()
The TI-89 has a sum function that will be used to define a new function r r s. This new function will accept the values of the endpoints of the interval [a, b] and the number of rectangles to be used, n, and return the total area of the right-hand rectangles that approximate the area under the curve defined by f(x).
- Execute NewProb to clear all one-letter variables
- Define f(x)=x^2
-
Define
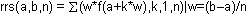
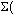 ,
,
the sum function, is the fourth entry in the Calc menu, which is accessed by pressing

The sum function 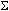 evaluates an expression at discrete variable values within a range and returns their sum. Its syntax is
evaluates an expression at discrete variable values within a range and returns their sum. Its syntax is
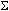 (expression, var, initial value, ending value).
(expression, var, initial value, ending value).



 .
.

The approximate areas returned by the function rrs are clearer if the results are given in decimals.
-
Set your calculator to Approximate Mode by pressing
 and selecting APPROXIMATE as the Exact/Approx option
and selecting APPROXIMATE as the Exact/Approx option
- Enter the command rrs(0,1,4)
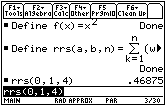
This is the same total area you found in the table using the four rectangles:
![]()
Using more Rectangles
You can use this function to approximate the area when the region is divided into more rectangles.
15.1.2 Use the function rrs to approximate the area under f(x) = x2 over the interval [0,1] using 10 rectangles, 50 rectangles and 100 rectangles.
Click here for the answer.
Converging Sums
If we continue to evaluate r r s (0, 1, n) for larger values of n, the sums will appear to converge to a limiting value. Evaluate the limit of r r s as n approaches
![]() .
.
- Set Exact/Approx back to AUTO Mode
-
Evaluate limit (rrs(0,1,n),n,
 )
)
The limit function is in the Calc menu and
![]() is above
is above
![]() .
.
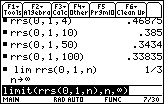
The exact area under the curve f(x) = x2 over the interval [0,1] is the value of the limit,
![]() square unit.
square unit.
Do not clear the memory or the History area of the functions you defined in this lesson so that they may be used in Lesson 15.2.
15.1.3 Evaluate r r s (0, 1, n) on the Home screen. What is the limit of this expression as n approaches infinity?
Click here for the answer.