Implicit differentiation, partial derivatives, horizontal tangent lines and solving nonlinear systems are discussed in this lesson.

Consider the folium x³ + y³ – 9xy = 0 from Lesson 13.1. How would you find the slope of this curve at a given point? As before, the derivative will be used to find slope.

Differentiating Implicitly

One method to find the slope is to take the derivative of both sides of the equation with respect to x. When taking the derivative of an expression that contains y, you must treat y as a function of x. This method is called implicit differentiation and it is illustrated below.

Implicit differentiation of the folium x³ + y³ – 9xy = 0 yields .

Notice that the term -9xy is considered a product of two functions and the Product Rule is used to find its derivative, .

Solving for

Solving the expression for gives the derivative:

Notice that the derivative contains both x and y. This is typical for implicit differentiation.

Using the TI-89 to Differentiate Implicitly

Another method used to find is with your TI-89 and the following theorem from calculus:

If z is a differentiable function of x and y such that z(x, y) = 0 defines y implicitly as a differentiable function of x, then at any point where

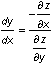
The symbol is called the partial derivative of z with respect to x. It means to take the derivative of z with respect to x while treating y as a constant. Similarly, is the partial derivative of z with respect to y. To find this partial derivative, take the derivative of z with respect to y while treating x as a constant.

Finding Partial Derivatives

With z1= x³ + y³ – 9xy, 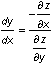    can be found on the TI-89 with the derivative command.

Notice that parentheses are used to indicate the variables x and y of the function z1.

• Enter -d(z1(x,y),x)/d(z1(x,y),y)

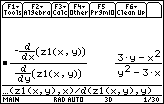
13.2.1 Using the expression shown above, find the slope of the line tangent to the folium at the point (4,2). Click here for the answer.

The graph of z1 shown in Lesson 13.1 suggests that one branch of the curve has a horizontal tangent at (0, 0) and another branch has a vertical tangent at (0, 0). The formula for dy/dx takes the form 0/0 at (0, 0).

Horizontal and Vertical Tangents If both the numerator and denominator of the formula for dy/dx are zero, the tangent(s) at that point can be horizontal, vertical, or neither, and the only way to tell is by looking at the limit.

Finding Horizontal Tangents

If the slope is zero, the tangent is horizontal, which happens when the numerator of is zero and the denominator is not zero.

Solving Nonlinear Systems of Equations

You can find the coordinates of the points on the folium in this case by finding the solutions to a nonlinear system of equations where one equation defines the set of points on the graph and a second equation defines the set of points where the derivative is zero. Solutions to the system below are the points on x³ + y³ – 9xy = 0 where the tangent may be horizontal.

x³ + y³ – 9xy = 0 and 3y – x² = 0

The solutions to the system can be found by using the Solve command to find values for the two variables x and y that make both equations true. Notice that parentheses are used to indicate that z1(x, y) is a function of x and y and that the variables to be found, x and y, are enclosed within braces.

• solve(z1(x,y)=0 and 3y-x^2=0,{x,y})

The braces are found above and .

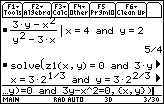
One of the two solutions is . You will need to scroll to the right in the History Area to see the other point, (0, 0). We can reject (0, 0) because this makes the denominator of dy/dx zero.

13.2.2 Show that the tangent is horizontal at the point found above. Click here for the answer.

Look at the graph of the folium to see if this point seems reasonable.

Finding Vertical Tangents

If the denominator of is equal to zero and the numerator is not zero, then the tangent is vertical.

The points that satisfy the system x³ + y³ – 9xy = 0 and y² – 3x = 0 are the points of the folium where the tangents may be vertical.

13.2.3 Find the coordinates of the points of the folium that satisfy the system above. Click here for the answer.

The figure below shows that dy/dx is undefined at

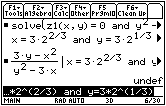
We need to know that the derivative is infinite at to have a vertical tangent. We can see this from the graph, so we have a vertical tangent at . Notice that the derivative is of the form 0/0 at (0, 0).

What Happens at (0, 0)?

We can see from the graph that there is a horizontal tangent and a vertical tangent at (0, 0).

Exploring a New Implicit Relation

The procedure used in the exploration of the folium will be used to investigate the implicitly defined relation y⁴ = y² – x².

Graphing the Relation

Gather all the terms to the left side of the equation: y⁴ – y² + x² = 0.

• Set z1=y^4-y^2+x^2
• Set the following Viewing Cube values:

eye = –90	xmin = –1.5	ymin = –1	zmin = –10
eye = 0	xmax = 1.5	ymax = 1	zmax = 10
eye = 0	xgrid = 14	ygrid = 14	ncontour = 5

13.2.4 Display the graph of the relation. Click here for the answer.

13.2.5 Find the slope of y⁴ – y² + x² = 0 at the point . Differentiate by hand then use your TI-89 to verify your result. Click here to check your answer.

13.2.6 Where is the tangent to y⁴ – y² + x² = 0 vertical? Use your TI-89 to view the graph and determine if the answers seem reasonable. Click here for the answer.