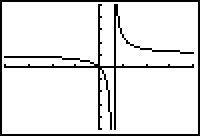
The vertical asymptote appears to be at about x = 3.

The horizontal asymptote appears to be at about y = 2.

As x approaches 3 from the left, the function values are negative with increasing magnitude. In other words, .

As x approaches 3 from the right, the function values become larger without bound. In other words, .

The tables show that as the magnitude of the x-coordinates increase, the y-coordinates get closer to 2.

and

Since the limit exists, x = -2 is not a vertical asymptote, but rather the x-coordinate of a hole. The coordinates of the hole are .

Because and there is a vertical asymptote at x = 2.

Because , there is a hole at (-3, 1.8).

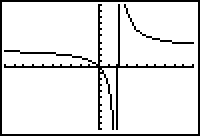
[-10, 10, 1] x [-10, 10, 1]	The Zoom Decimal window

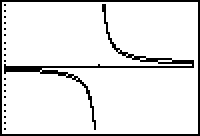
Because is a vertical asymptote, y = x + 2 is an oblique asymptote, and the graph of resembles near x = 2.

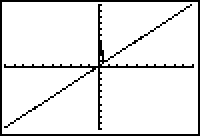
Y1 = (X2+1)/(X-2) Y2 = X+2 [-100, 100, 10] x [-100, 100, 10]	Y1 = (X2+1)/(X-2) Y2 = 5/(X-2) [1, 3, 1] x [-100, 100, 10]

The rational function has a vertical asymptote at x = 2. The polynomial y = x² - 8x - 15 is a nonlinear asymptote for the rational function and the function resembles near x = 2.

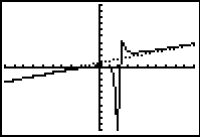
[-10, 10, 1] x [-100, 100, 10] Xres = 2